By Lambert Strether of Corrente.
Patient readers, I have had a complexified day, and so today’s Water Cooler will be a bit abbreviated. A shame, since there’s so much happening! –lambert
Politics
“But what is government itself, but the greatest of all reflections on human nature?” –James Madison, Federalist 51
“They had one weapon left and both knew it: treachery.” –Frank Herbert, Dune
2020
Booker:
Cory Booker on the filibuster to @NPRinskeep: “We need to understand that there’s good reason to have a Senate where we are forced to find pragmatic bipartisan solutions. Let’s be a country that operates from that sense of common purpose.”
— Alex Seitz-Wald (@aseitzwald) March 7, 2019
Booker wants to take office. But he doesn’t take power, does he?
Sanders: “Bernie Sanders Is Beating Kamala Harris 2-1 Among Black Democratic Primary Voters, New Poll Finds” [The Intercept]. “Bernie Sanders is leading all other announced candidates in support from black voters, a new poll [from Morning Consult] finds. Sanders’s support among black voters, at 28 percent, puts him in second place among that demographic, behind Biden, at 32 percent. He trailed Biden 31-25 among whites.” And about class:
There appears to be a strong class element at play in the finding. The same poll found that the demographics Sanders is least popular with — at 19 and 17 percent, respectively — are Democrats who make more than $100,000 per year and Democrats who have post-graduate degrees (two qualities that typically, if not always, overlap). Because of structural wealth and income gaps, that population is heavily white.
Sanders, meanwhile, receives his strongest support support from those making less than $50,000 — a group that is, for the same reasons, much more diverse. The poll found that 30 percent of those with the lowest incomes backed Sanders.
In other words, Thomas Frank is right. The professional class hates Sanders — and they are the base of the Democrat Party.
* * * “The Bernie-Hillary Feud Is Bleeding Into 2020” [Talking Points Memo]. “Clinton allies were irritated that Sanders made former Ohio State Sen. Nina Turner a campaign co-chair, since she pointedly refused to endorse Clinton during the 2016 general election.” • “Listen to black women,” lol.
“Sanders vs. Clinton: 2016 rivalry proves hard to overcome” [Associated Press]. “Bill and Hillary Clinton don’t believe Sanders can beat Trump, according to people who have spoken to them and requested anonymity to discuss private conversations.” • And the Clintons tend to act on their putative beliefs, don’t they?
The DCCC is still at it:
@dccc is this yours? I hope not. If so, are you serious? Staying neutral? Where is @BernieSanders name? And don’t blame it on an intern. This is more of the shame underhanded foolishness from 2016. #BERNIE2020 pic.twitter.com/70Jj6Ec7q8
— Nina Turner (@ninaturner) March 4, 2019
2019
“Pelosi: House anti-hate resolution won’t mention Omar” [Associated Press]. “Pelosi defended Omar and says she does not believe the new congresswoman understood the ‘weight of her words’ or that they would be perceived by some as anti-Semitic. ‘It’s not about her. It’s about these forms of hatred,’ Pelosi told reporters.” • A courageous stand indeed! Remember that bucket of warm spit, “Love trumps hate” from the Clinton campaign? Consistent messaging is everything. Because bad things are bad:
Please support HR 2, the We Condemn All Bad Things And In No Way Should This Be Interpreted As Throwing Shade At Anyone In Particular Act of 2019
— David Burge (@iowahawkblog) March 7, 2019
“The left’s revolt against Democrats’ plan to punish Rep. Ilhan Omar appears to be working” [Vice]. “Democrats seem to have underestimated the groundswell of support that manifested for Omar. Engel, chair of the House Foreign Affairs committee, vowed not to kick Omar off the committee and started defending her on Twitter. Even one of Omar’s defenders, Rep. Alexandria Ocasio-Cortez, received backlash for not being explicit enough about her defense of Omar.” •
“Political operation tied to Alexandria Ocasio-Cortez aide faces scrutiny” [CNN]. “Saikat Chakrabarti’s corporation, Brand New Congress LLC, received $867,000 in 2017 from two political action committees he helped found, Brand New Congress PAC and Justice Democrats, Federal Election Commission records show. Ocasio-Cortez’s campaign also paid Chakrabarti’s corporation more than $18,000 in 2017 for ‘strategic consulting.'” • $18,000? Really? That’s hardly enough to buy a parka for Bernie. What’s wrong with these people?
Health Care
“Lobbyist Documents Reveal Health Care Industry Battle Plan Against ‘Medicare for All'” [The Intercept]. I ran this when it appeared in November 2018, but with HR1834 out, it’s worth a second look: “‘We’re all focused on 2020,’ Lauren Crawford Shaver, a partner at Forbes-Tate who is helping to manage the [Partnership for America’s Health Care Future] campaign, recently told the National Association of Health Underwriters in a podcast produced by the group. Shaver, a former top staffer for the Hillary Clinton presidential campaign explained to the group that she is working to peel support away from the ‘Medicare for All’ bill sponsored by Sen. Bernie Sanders, I-Vt.: • “Never, ever.”
Realignment and Legitimacy
“In search of a new center in the culture war” [Damon Linker, The Week]. “For much of the past four decades, the American center has been defined by its broadly libertarian outlook on both economic and social issues. To be a centrist Democrat, a centrist Republican, or a centrist independent has been to favor keeping taxes relatively low, regulations relatively minimal, international trade relatively free, and government services and benefits intact and in place while not expanding them very far into new areas. It has also meant supporting abortion rights and eventually gay marriage and transgender rights, and favoring, for both moral and economic reasons, high levels of immigration. Yet a comprehensive survey of voters in the 2016 election has revealed that very few people actually support this combination of libertarian policies — and that lots of people favor the ideologically opposite position: relatively progressive on the economy and relatively conservative on social issues.” • Hoo boy.
“Reading Mobilization” [Inside Higher Ed]. • Interesting discussion of the difference in signage between the 1963 March on Washington, and the National Women’s March. In 1963: “The organizers kept the event unified and on message through printed signs calling for school integration, full citizenship, a higher minimum wage and a few other agreed-upon demands. No unauthorized placards were allowed.” So no debacles like: “If Hillary were president, we’d be at brunch right now.” Iconic though that was.
“Open the Jeffrey Epstein files. All of them.” [WaPo]. “It is time to uncover all the hidden secrets in the sordid matter of Jeffrey Epstein, the wealthy sex offender with a stable of high-placed friends. Pull up the floorboards and see what slithers or scurries into the light… For example: What do the FBI and Main Justice know about the strange failure of New York’s district attorney to vigorously investigate alleged sex trafficking at Epstein’s Manhattan townhouse and “modeling agency”? What have the feds heard about Epstein’s conduct at his New Mexico ranch and aboard his private jet? Has there been any contact with law enforcement in the U.S. Virgin Islands, where Epstein owns a private compound visited by the likes of former president Bill Clinton and numerous rich-guy moguls?” • Sounds bipartisan!
Stats Watch‘
Productivity and Costs, Q4 2018: “A key vital sign for the U.S. economy is favorable as nonfarm productivity rose at a higher-than-expected annual rate” [Econoday]. “However you look at it, U.S. output is growing at a healthy rate and wages, as cited by Jerome Powell, are beginning to show improvement.”
Challenger Job-Cut Report, February 2019: “The number of layoff announcements has clearly shifted higher through the end of last year and into this year” [Econoday]. “But actual layoffs following announcements of layoffs can take months which may be good news for the near-term jobless claims and employment reports but this delayed effect poses a risk for reports through the first half of the year.”
Jobless Claims, week of March 2, 2019: “February was yet another strong month for the labor market” [Econoday]. “No states were estimated in the week and there were no special factors. Whatever the questions over retail spending or bumps underway in the factory sector, demand for labor remains very strong.”
Retail: “One stat in Target’s earnings proves stores are still the biggest defense against Amazon” [Business Insider]. “In the company’s latest earnings report, Target says it fulfilled nearly three out of every four digital orders through its stores in some way…. ‘Digital growth at Target isn’t coming at the expense of our stores,” [CEO Brian Cornell] told investors on Tuesday in a meeting. ‘It’s making stores more relevant.'”
Retail: “NCAA Judge Goes Easy on Convicts, Hard on College Basketball” [Bloomberg]. “Two weeks before the annual college basketball tournament known as March Madness, U.S. District Judge Lewis Kaplan sentenced former Adidas AG executive James Gatto to nine months, while Merl Code, a consultant with ties to Adidas, and agent Christian Dawkins each got six…. The three were convicted of conspiring to defraud universities by routing payments to the families of recruits and concealing those payments from the schools. Meeting in parking lots and hotel rooms, they hustled cash to family members of hot prospects, who in turn joined college programs sponsored by Adidas.” • Universities shouldn’t be in the sports business.
Tech: “Stalkers and Debt Collectors Impersonate Cops to Trick Big Telecom Into Giving Them Cell Phone Location Data” [Vice]. “Bounty hunters and people with histories of domestic violence have managed to trick telecommunications companies into providing real-time location data by simply impersonating US officials over the phone and email, according to court records and multiple sources familiar with the technique. In some cases, these people abuse telecom company policies created to give law enforcement real-time location data without a court order in ‘exigent circumstances,’ such as when there is the imminent threat of physical harm to a victim. The practice is ongoing according to the sources, and court documents and an audio recording obtained by Motherboard also detail a previously prosecuted case in which one debt collector tricked T-Mobile by fabricating cases of child kidnapping to convince the telco to hand over location data.”
Tech: “Facebook’s reputation is sinking fast” [Axios]. • From the Axios Harris Poll RQ ranking, 2012–19, “Public reputation of the 100 most visible U.S. companies.: In 2012, Facebook ranked #51. Now it ranks #94.
Tech: “A Privacy-Focused Vision for Social Networking” [Mark Zuckerberg, Facebook]. “Over the last 15 years, Facebook and Instagram have helped people connect with friends, communities, and interests in the digital equivalent of a town square. But people increasingly also want to connect privately in the digital equivalent of the living room. As I think about the future of the internet, I believe a privacy-focused communications platform will become even more important than today’s open platforms.” • I would totally trust Facebook in my living room. Who wouldn’t?
Tech: “Facebook’s pivot to privacy has huge implications — if it’s real” [The Verge]. “Zuckerberg is fond of grand pronouncements — it’s less than four years since he declared that the News Feed would one day primarily be video, and just two years since he announced that Facebook would concentrate on “developing social infrastructure,” whatever that might have meant. In any case, neither vision came true. Whether this one does, facing even longer odds, remains anyone’s guess.”• Plus the stock didn’t move.
Tech: “Zuckerberg says Facebook’s future is going big on private chats” [Reuters]. “James Cordwell, a financial analyst at Atlantic Equities, said Facebook’s strategy risks undercutting its current way of making money. ‘But if they can pull off this WeChat-esque strategy,’ he said, ‘it could open up material revenue streams beyond just advertising, something that investors have been craving for quite some time.'”
Manufacturing: “Made for Next to Nothing. Worn by You?” [New York Times]. “Home work — working from home or a small workshop as opposed to in a factory, often for a subcontractor who is then employed by a supplier for an established company or brand — has long been a cornerstone of the fast-fashion supply chain. It is particularly prevalent in countries such as India, Bangladesh, Vietnam and China, where millions of low-paid and predominantly female home workers are among the most unprotected in the industry… In northern India, where most of the 1,452 workers interviewed were located, about 76 percent started their home-based work because of “some form of duress,” including severe financial hardship, family pressure or lack of alternate income. The youngest individual interviewed was 10 years old; up to 19 percent of the workers were between 10 and 18 years old.” • Not good at all, but let’s not forget that “some form of duress” includes wage work as such, and that’s not a bug, it’s a feature.
Concentration: “The case against Amazon” [Politico]. “European Commissioner for Competition Margrethe Vestager is guarded about the nature of her investigation, but has stressed that it focuses on data usage and the way that Amazon has a hybrid role as both a shop and a platform for other sellers. The central point to investigate would be whether Amazon abuses its dominance of online retail to collate useful data from competitors and then uses that same data to push sales of its own wares.” • Lots of anecdotal data about this. So if Vestager is on the trail…
The Biosphere
Only 80 days ’til Memorial Day, when Maine puts the seeds in the ground!
am going to start from seed: peas, cucumbers, zucchinis, leeks, big sauce tomatoes and little cherries, sweet basil, and fennel. i'm direct sowing sunflowers, beans, fernleaf dill, salad greens, rainbow carrots and parsnips. i'm only buying strawberry starts and seed potatoes.
— sweet cicely ? (@spindlypete) March 6, 2019
I strongly advise readers who grow vegetables, especially readers starting out, to grow from seed. It’s not hard; after all, seeds are highly adapted to growing, so the only real requirement is patience (and, in Maine, not getting over-optimistic and planting too early). Only after I became a little time-pressed, and bought flats (“starts”) of plants at the Farmer’s Market, did I get bugs, and after I got bugs, I never got rid of them (because I don’t want to use sprays, and who has the time to look for eggs on the underside of leaves?). So I dropped vegetables, and moved over to flowers — an approach that has many other advantages — but that’s not exactly Jackpot-ready behavior, now is it? Oh, and a garden affects everything around you, everything, I would argue for good. Critters, neighbors, even the the air and water. It’s not at all like changing personal consumption habits.
Macroni is anti-food:
Soylent is to humanity what macaroni is to Georgians. pic.twitter.com/g7qoXIPgmK
— Frédéric Leroy (@fleroy1974) February 21, 2019
Water
“Radium contamination in public water systems nationwide” [Environmental Working Group] (methodology).
Guillotine Watch
“Here’s Where to Find the World’s Super Rich, From Paris to Tokyo” [Bloomberg]. “The world had almost 200,000 ultra-high-net worth individuals last year, according to the broker’s wealth study, with more than two-thirds of them across Asia, Europe and North America.” Handy map:
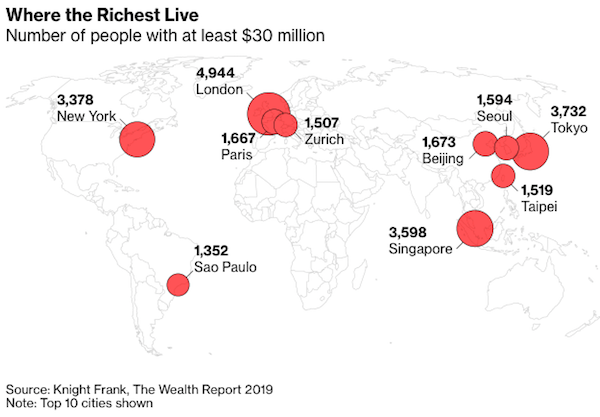
“Can a Hedge Fund Quant Remake a City Without Destroying It?” [Bloomberg]. No. More: “What Woodriff really wants to do with his wealth is transform Charlottesville into a place that will attract more people like, well, him.” As I said.
News of the Wired
Look how “smart” this lock is:
Everything is fine. https://t.co/OJ9tjjYgeD pic.twitter.com/clQuaKUrrp
— Network Security Engineer. Architect. Leader. (@vipergts46) March 6, 2019
Readers, feel free to contact me at lambert [UNDERSCORE] strether [DOT] corrente [AT] yahoo [DOT] com, with (a) links, and even better (b) sources I should curate regularly, (c) how to send me a check if you are allergic to PayPal, and (d) to find out how to send me images of plants. Vegetables are fine! Fungi are deemed to be honorary plants! If you want your handle to appear as a credit, please place it at the start of your mail in parentheses: (thus). Otherwise, I will anonymize by using your initials. See the previous Water Cooler (with plant) here. Today’s plant (MR):

MR writes: “One of the many pollinators that’s hanging out at my trailing indigo.” Good news about pollinators!
Readers: Water Cooler is a standalone entity not covered by the annual NC fundraiser. So do feel free to make a contribution today or any day. Here is why: Regular positive feedback both makes me feel good and lets me know I’m on the right track with coverage. When I get no donations for five or ten days I get worried. More tangibly, a constant trickle of small donations helps me with expenses, and I factor that trickle in when setting fundraising goals. So if you see something you especially appreciate, do feel free to click below! (The hat is temporarily defunct, so I slapped in some old code.)
Or Subscribe to make a monthly payment!


RE: Sanders (lack of) support: Democrats who make more than $100,000 per year and Democrats who have post-graduate degrees (two qualities that typically, if not always, overlap).
Yeah, I can personally verify that – the part in parentheses, that is.
Lol are you, like me, a professor of the humanities?
Guess that makes be a double oddball.
I fall under both categories. Many in my cohort shake their heads and sigh when I open my mouth. I must be crazy to reject the received wisdom.
It is impressive, and apparently rare, to have maintained skepticism through so many years of indoctrination!
You double winners need to start a “Class Traitors for Sanders” meme or something.
The disgust is much more visceral at $200K and up
The spouse’s fancy law firm parties are a social minefield for this public defender. When I mentioned Sanders I was asked in a shocked, horrified tone if I hated rich people. Well at this point yes you are getting a bit grating, Karen.
Just got a card in the mail from the DSA for a poll on whether to endorse Sanders for President.
My take is “yes, certainly; who else?” No time for keeping one’s powder dry, unless this would
create some strategic problem I haven’t thought of.
The issue at hand for DSA is not who, but when. Delaying endorsement means keeping resources free to support other, more diverse work that only DSA does, while Sanders seems to have enough early to support as the primary season begins.
There won’t be other applicants? Like, for instance, a Green? (Don’t look at me – I have no clue who that might be.)
I received an email from DSA National. I voted F YES!
As much as I would prefer to see Sanders as President, I think that it would be a mistake for DSA to endorse anyone for President at this point. The organization needs to continue to build itself as a distinct political entity, particularly at the local level. Endorsing now could pull them into the Democratic / Republican dynamics at the national level, when they’re not strong enough to stand apart from either party.
Exactly.
Yes. And why not Gabbard, whose social democratic bona fides are about what Bernie’s are? Well, absent the years of consistent advocacy that make Bernie especially credible.
Well, for me, the answer is in your last sentence. Like what she’s *saying*,
sent her money to hopefully get her in the debates, but the rest is under review.
Sanders easily has more credibility than all the other candidates. (Warren or Gabbard come in second.) MSM is inclined to lump all the candidates together, saying that most of them are on board with Sanders’ agenda and that’s why he’s going to find it difficult to compete. But many of us on the left who fell for Obama’s hope and change now look more closely at the correspondence between a candidate’s words and deeds, as well as the consistency of and reasoning behind her/his positions. Perhaps more important, unlike with our support for Obama, we are now moved to take a close look at a candidate’s donors. If you say you’re for Medicare for All, but you’re taking lots of money from Wall Street and the Healthcare industry, you’re just not worth trusting. As for Gabbard, I’d love to see her as Sanders’ Secretary of Defense.
She’s not a long time progressive, but now moving left. And only polling 1% in latest…
IMO best to focus on Bernie as best shot to win dem nom and general.
I agree, especially with regard to the general — just can’t see one of the other candidates gathering as much support as Sanders. But, of course, dirty politics….
Booker literally sounds like a US Chamber of Commerce spokesbot. From Marketplace in January:
Gillibrand: “not a contradiction” to call for universal healthcare while taking money from drug companies.
Harris: What do the American people want from their leader? …What they want to know is that people who want to be the leaders of this country are actually seeing them and thinking about the issues that keep them up at night. That’s what they want. And whoever has the best plan for that, and I think speaks most truth about the reality of American life today, and speaks truth and with an honest heart and purpose about what can be the vision for our country…
Booker: We need to understand that there’s good reason to have a Senate where we are forced to find pragmatic bipartisan solutions. Let’s be a country that operates from that sense of common purpose.
And don’t get me started on Biden. Or Sherrod Brown or Amy Klobuchar or any of the other phonies. One could describe their campaign rhetoric as “shallow”, or “wordsalad”. My grandfather raised cattle and used much more colorful descriptions. The proper rispote to politicians like this is: “what exactly do you propose to do?”
Harris: What do the American people want from their leader? …What they want to know is that people who want to be the leaders of this country are actually seeing them and thinking about the issues that keep them up at night.
Harris has racial blinders and a chocolate chip on her shoulder. Kamala sees whites and especially white males, except her corporate donors, as the enemy.
That’s her business, but don’t expect us to prefer her to Trump.
Tulsi Gabbard, however, is a woman of color I would vote for and salute.
I hadn’t thought of it before. I would have no problem saluting Major Gabbard. None of the rest. I haven’t decided if I will vote for her or Bernie Sanders in Maryland’s primary.
It’s very, very hard to believe that Biden is polling above Sanders with black voters.
“Jail ’em” Joe? Mmm.
I think at this point it’s a lot of name recognition. But black people are not a monolithic block and anybody who thinks they are should beware of Hillary’s fate.
Agree with you. Name recognition. Each of us has a responsibility to show and tell everyone who will listen that Big Finance OWNS good ‘ole Joe.
Name recognition and the lingering effect of being the VP for President Clean B.* Articulate.
*Bright
When re runs, will it be Harris who takes the hatchet to him (given the results of the Morning Consult poll)?
But they did enough for her in SC to derail Bernie.
And now preferring Biden?!?
Doesn’t seem to be in their own interest, but history could repeat… and then Biden loses to trump.
And dem elites win.p because Bernie defeated.
Not really. Black voters, at least at this stage, are very much in line with the dem base electorate at large.
Keep in mind, we’re all basically political junkies on this site, most voters haven’t started paying close attention, yet, since we’re a year out from any primaries. Biden still has a halo effect lingering from pleasant coverage from DC press core and from nostalgia for Obama. Much like Clinton did….he’ll start dropping as soon as he starts campaigning.
I thought it was very interesting that the entire focus group on CNN yesterday was unanimously, emphatically a “NO” on Joe Biden. I was taken aback by that.
Anita Hill. Bankruptcy bill. Aiding the rightward lurch of the Senate for 30+ years.
I mean this seriously: What’s to like?
I can say this, I’m happy to be a class traitor in my support of Sanders. If only we had some class traitors with actual power.
Might be a good time to pick up the uber-elite-bat-phone and give Nick Hanauer a call and see if he’ll back Bernie too.
I’m still 100% sure that regardless of popular support, and with as many donations as he can take, they will still screw him in the primary.
As long as the fix is in at the ballot box, nothing else really matters. I don’t get fooled twice. I won’t play football with lucy, I’m not Charlie Brown.
“One must imagine Sisyphus happy.” – AC
First, assume a flat hill.
Don’t be rude about Hillary. /s
A case of Leased Majesty.
Article in a local paper last week about how the State has been urging districts to buy electronic voting machines before the primaries. So they are, and then finding out that the $4M pricetag is only subsidized by the State for $1M and they are scrambling to finance the rest of the tab over 10+ years because no one has the budget.
There’s no money for (insert favorite public expenditure) but they are ordering computerized voting machines without knowing how to pay for them. Nothing to see here.
The purpose of having so many candidates from geographically distant states is to allow some combination of them to win enough votes in the primary to force a second ballot during the convention. At which point the superdelegates work out the grand compromise corporate candidate and Bernie refuses to do anything about it.
Way too plausible.
Those who imagine themselves to be our betters would do well to recall JFK:
“Those who make peaceful change impossible make violent change inevitable.”
Guess I’m a class traitor too!
I prefer to think of myself as “not a f#$king idiot” as opposed to a class traitor.
Anybody making less than a million a year that thinks they are “an elite” and protected from bankruptcy by being sick or homelessness by losing a job was not paying attention in 2009, and is an idiot.
I mean, they’re colluding against baseball players to suppress their salaries…they have literally run out of Americans to fleece and have moved on to the multi-hundred-thousand-aires and millionaires.
Being a billionaire is a character flaw. Any society that allows them to exist is diseased.
Agree. I grow stuff so the children and now the small grandchildren can forage in the fresh fruits and vegetables. Without washing anything.
You can use some soap mixed in water and spray with that. There is special “insect soap” for this, the brown “crystal soap” one use on floors will work well enough too.
One can also buy live mites, wasps, and other insect predators. These are best for greenhouses. These will stick around if one doesn’t clean too much.
Finally, quails are good for eating larvae and such off plants close to the ground. More work though, my financial advisor swore by them.
With time and experiment one will gets some kind of ecosystem going and there will still be some residual insect attack but not enough to really do damage.
The grandkids will eat up everything though.
Thank you. Reminds me of going out to the garden and finding my son (about 2) and his little friend sitting there systematically eating the peas.
As well as our dog, several years later, pulling up carrots and eating them.
Good memories.
>The grandkids will eat up everything though.
Yeah humans are the very top of the pest chain, aren’t they? :)
One could consider that Lambert’s bugs in question could very well be food for other, often beneficial, insects. Sometimes, you just have to except the circle of life, and relinquish control ! And if your goal is to creat a diverse biota, within one’s confines, then you have to expect the supposed ‘bad’ with the ‘good’ !
I will keep trying to grow things from seeds. My efforts so far have been… humbling.
Don’t get seeds from the big box stores – they are absolute garbage. Instead, take a look at Johnny’s or FedCo.
Pinetree Seeds in Maine is a great outfit. More seeds and less $$ than others generally.
It’s not so easy.
Mentioned this the other day when Lambert gave them a shout out – Dr. Bronner’s soap with water works great on caterpillars. I use it on the sawfly larvae on my azalea and also on the broccoli worms. Be sure to use it repeatedly, especially after it rains.
I made the mistake many years ago of using one of the more potent insecticide on caterpillars. I forgot that with no caterpillars there are no butterflies.
This is “a bit abbreviated”? Seems like a pretty substantial day’s worth of good reads to me, like most Water Coolers. Methinks your apology unnecessary.
However, shouldn’t today’s “News of the Wired” be filed instead under “Internet of **it”?
Could it be that Facebook’s supposed turn to private communications anticipates a possible move by lawmakers to finally recognize that Facebook and other social media are, in fact, publishers and not platforms?
This would be premised on the fact that these outfits are clearly editing, censoring and otherwise being selective about the content they allow. Thus they are publishers, and equality before the law would subject them to the same defamation liabilities that all other media are subject to — destroying the existing social media business model.
Private communications, however, could exempt them from such liabilities.
Facebook’s private conversations are not so private.
Facebook uses the caller/called, the metadata, information to build a maps of who knows who.
Encrypting the content is only one part of privacy. Effectively mapping “known associates.”
“They trust me with their data. Dumb f**ks.” – Zuckerberg
” where Epstein owns a private compound visited by the likes of former president Bill Clinton and numerous rich-guy moguls?”
And Dershowitz.
I was thinking, because I couldn’t help it, about why Acosta would have made such a point of letting Epstein off so lightly. Sure, he’s rich, but a pedophile? Normally prosecutos come down heavy on that. And I think the answer has to be political pressure, and specifically one name: Bill Clinton. Even though Acosta appears to be a Republican.
So granted this reflects my priors, but I think Slick Willy was in it up to his you-know-what. Starts with w. He does have quite the reputation.
“Sanders vs. Clinton: 2016 rivalry proves hard to overcome” [Associated Press]. “Bill and Hillary Clinton don’t believe Sanders can beat Trump, according to people who have spoken to them and requested anonymity to discuss private conversations.” • And the Clintons tend to act on their putative beliefs, don’t they?
—-
It’s good Sanders is not interested in seeking advice from Hillary.
I wonder if he will say the same about seeking Obama’s.
Both Barrack and Hillary are equally likely, more or less, to offer this really useful advice, ‘Don’t be like me.
Perhaps to pre-emp any accusation that Sanders rejects only women (Hillary among them) and not men (Obama being one of them), he could also calm many of us by stating publicly about not seeking Barry’s.
I don’t Sanders has anything to worry about in regards to Joan, of Ark.
Joan, of Ark.
She was not the same as Jan, of Hus?
Sorry, you see the way the way the joke is set up, HRC can either be a heroine who saves us from ourselves, or merely a denizen of the Razorback state and possibly living in a tornado-prone mobile home.
I am sorry too, as Joan’s tragedy reminded me of another one (Jan’s), and those two unforunate events so distracted me that I failed to pick up a good joke.
“Over the last 15 years, Facebook and Instagram have helped people connect with friends, communities, and interests in the digital equivalent of a town square. But people increasingly also want to connect privately in the digital equivalent of the living room. As I think about the future of the internet, I believe a privacy-focused communications platform will become even more important than today’s open platforms.”
Signed
Cleetus “”Cowboy” Jones
Tyrone Williams
Think it wouldn’t be regulates to high heaven?
Whatever happened to just plain old talking to each other? Y’know, face to face?
What’s that?
:-)
More seriously, when I was in college like 20 years ago people were outside when the Sun was out reading books or talking or even frisbeeing. Nowadays I leave class and everyone is looking down at their device completely ignoring what’s around them and the students standing right next to them.
Honestly, it is very disturbing to watch.
“..Honestly, it is very disturbing to watch.”
Agreed, especially seeing a young “couple” fixated on their respective,
glowing screens, instead of the person they’re with.
This won’t end well.
Maybe the “real” couple were the ones that each of that pair were talking to on their screens.
So that would be why people aren’t having sex as much – you sort of have to relate to do that.
But it’s still a sign of a more and more alienated society.
Plus, the nature of what sex is getting done seems to be changing. Porn use among males can lead to a fantasy objectification of women and consequent dehumanization of the female. Undoing all those centuries of the ‘civilizing’ of the Male.
We are drifting into a “Rape Culture.”
Short form: What kind of sex?
I’ve noticed we don’t do a lot of physical things anymore, such as dancing, or whistling, or skipping while walking, or any number of little acts we used to do.
I was always inclined to dismiss the impact of smart phones because I’ve never had the slightest desire to own one
but you are absolutely right
the world has completely changed from under our feet
and people are fundamentally different with each other, in public at least
this is the biggest change in us culture since the turn of the century
well, that along with the extreme concentration of “news sources”
and the unprecedented levels of propagandistic noise that we endure
Dunno what other readers have found, but I see way less intense engagement with cell phones here in Birmingham, AL (on a visit now), than in NYC. The suburb my mother lives in is affluent and it scores as one of the top 100 in the US, as measured by density of BAs in the population, so don’t project My Cousin Vinny prejudices.
For instance, in my gym in NYC, most people who are weight training have headphones on, so it’s hard to politely ask them to let you work in when they are resting at busy times. The ones who aren’t listening to music often turn straight to their phone between sets….which leads to longer rests and more need to bug them to share.
In the Birmingham gym, headphone use is rare, hardly anyone checks their phone during workouts (they do while on the floor but usually in a sitting area) and people actually talk to each other.
In a gym in Topsham, Maine, I also saw very little cell phone engagement during weight workouts.
Anyone else see regional variations?
Cell phones are NOT ALLOWED at my fitness center. The folks with the bigger muscles enforce the rules.
Members are not using them for calls. They are using them to surf the web and listen to music. I go to a lot of gyms because travel and have seen only prohibitions on making and receiving calls, not accessing the Web. I find it hard to think that that’s restricted, given how many people I see using fitness videos to guide their workouts or using apps to record their workout (a big deal for serious bodybuilders).
Blue collar gym in Northern Cal: about 1/3 on phones, mostly music or workouts. Rarely and not encouraged are actual calls.
Almost all 20 somethings on phones. Oldsters up to early 80s almost none on phones.
Yes, I work in Public schools and the degree to which children are screen captured is…well, disturbing is not a strong enough word. This situation does not cause one to hold much optimism going forward.
I believe that so-called smart phones are a direct cause of developmental and social delays.
What’s even more depressing is how few parents seem to want to do anything about it.
“Political operation tied to Alexandria Ocasio-Cortez aide faces scrutiny” [CNN]. “Saikat Chakrabarti’s corporation, Brand New Congress LLC, received $867,000 in 2017 from two political action committees he helped found, Brand New Congress PAC and Justice Democrats, Federal Election Commission records show. Ocasio-Cortez’s campaign also paid Chakrabarti’s corporation more than $18,000 in 2017 for ‘strategic consulting.’” • $18,000? Really? That’s hardly enough to buy a parka for Bernie. What’s wrong with these people?
—
The amounts are secondary to the key question, ‘How much work or productive work, did each get back in exchange for the payment?’
He might have produced work worth more than $18,000 for that payment, or worth zero for the same amount.
But we are not told (at least not informed from the quoted passage).
There is a lot of smoke here, and not much firefighting. Chakrabarti tweeted out a nothing to see here summary with this link:
https://justicedems.freshdesk.com/support/solutions/articles/33000223353-when-i-look-at-the-fec-report-for-justice-democrats-in-2017-why-are-there-so-many-expenditures-to-b
It doesn’t explain where the money went.
It also appears AOC is one of three listed on the board of Justice Dems PAC which could be a really big problem for her. If she had a controlling interest in that PAC, which FEC forms say she did, while she was running her campaign and receiving funds from them, which isn’t totally clear, then she faces civil penalties. If she did so knowingly to circumvent campaign finance laws she faces prison time. AOC has been radio silent on both issues.
https://dailycaller.com/2019/03/04/ocasio-cortez-justice-democrats/
The first story was broke by Washington Examiner owned by Phillip Anschutz. The Daily Caller was started by Tucker Carlson and is financed by Foster Friess. The billionaires are going after her.
People make mistakes all the time.
It doesn’t have to be intentionally, on purose or knowingly.
Re. Epstein: so is Dersh going down? Jeffrey Epstein, Alan Dershowitz, and Pals Accused of Sex-Trafficking Ring.
Judging from the photo at the top of that article, it may be time to add a verse to “Ten Thou…” Better make it in Latin. Otherwise, it will be x-rated.
Key takeaway.
How is this guy still walking around? Guess we should ask Dersh, his onetime lawyer.
I’m wondering just how much “agency” a twelve or thirteen year old girl, or boy for that matter, has in sexual matters. In bygone days, this crime was accurately referred to as ‘White Slavery.’ Of course, in America a hundred and fifty years ago, the same happened to non-whites, in the guise of formal slavery. Much earlier, slavery was equal opportunity.
The entire Epstein imbroglio reminds me strongly of a De Sade novel. De Sade was a decadent French petty aristocrat before and during the French Revolution.
As for “…Dersh, his [Epstein’s] onetime lawyer,” lawyers are often the ‘bagmen’ and extra legal compradores of the wealthy.
This is revelatory:
“For much of the past four decades, the American center has been defined by its broadly libertarian outlook on both economic and social issues. To be a centrist Democrat, a centrist Republican, or a centrist independent has been to favor keeping taxes relatively low, regulations relatively minimal, international trade relatively free, and government services and benefits intact and in place while not expanding them very far into new areas. It has also meant supporting abortion rights and eventually gay marriage and transgender rights, and favoring, for both moral and economic reasons, high levels of immigration.”
—
It’s revelatory because no one outside the beltway bubble *ever* thought that was the “center”. Some people thought the civil rights/immigration was very leftie (though it was actually Liberal and libertarian; capital doesn’t care what color/gender/who you love are) and the tax/regulations/trade was seen as right wing/conservative (though it was also Liberal in some ways.) The governing elite took stuff from the right of them and unrelated stuff from the left of them and decided they were centrist. They did this because they were funded by the billionaire class (starting with the hard right Mellon Scaife Koch, funneled through the think tank industry and increasingly universities.)
(note “government services and benefits intact” has been a moving target; in the 4 decades he cites, we’ve had “welfare reform” of multiple types and “centrist” efforts at a “Grand Bargain”.)
Therefore, this bit should surprise no one outside the bubble:
Yet a comprehensive survey of voters in the 2016 election has revealed that very few people actually support this combination of libertarian policies — and that lots of people favor the ideologically opposite position: relatively progressive on the economy and relatively conservative on social issues.”
Indeed, the relatively conservative on social issues is not surprising given the Rs’ deliberate empowerment of the religious right for the past couple of decades…
“:What’s the Matter with Kansas” – answer: no one was offering them progressive economic policies, so they went with conservative on social issues.
However, actual polling shows that those people are far from a majority, except on immigration – which is also an economic issue. Apparently the great unwashed do grasp the concept of supply and demand.
Re; “Pelosi: House anti-hate resolution won’t mention Omar”
“Hate” was once a powerful descriptive word. Lately, it has been co-opted by The Liberals to mean, “Not on Our Team”. To conflate simple criticism of Israel with the Holodomor, the Holocaust, African Slavery, The Armenian Genocide, The USAian Opioid Epidemic……..shows a terrible, (but typical) moral disengagement from the tragic deaths of millions. “We are living in our own private fantasy World. We built it All-By-Ourselves, with our (Mr) Clevver, rational minds!”. ha
Gutted of it’s traditional meaning, the word, “Hate” has been transformed into a Corporate Logo, (much as Coco Cola has appropriated Santa Claus to advance it’s sweet caffeine agenda……) As soon as I hear or read “hate/hateful”, I know that it is a TradeMarked, Corporate Signifier of stern disapproval.
“10 English Words That Have Completely Changed Meaning”
https://theculturetrip.com/europe/articles/10-english-words-that-have-completely-changed-meaning/
“Awful
In Old English, ‘awe’ referred to “fear, terror or dread”. This later morphed into a solemn or reverential wonder, and ‘awful’ and ‘awesome’ were synonymous with awe-inspiring. Later, ‘awful’ took on a solely negative connotation…….
Cute
A shortening of the word ‘acute’, ‘cute’ originally meant sharp or quick-witted…”
I just want to say that the Holodomor isn’t a thing. Not that millions of Ukrainians didn’t starve to death, they did. But it was part of a pan-Soviet famine largely brought on by forced farm collectivization. Ukraine wasn’t even the worst affected region. The idea of some sort of deliberate, targeted genocide of Ukrainians is simply untrue.
Denial of the Holodomor
https://en.wikipedia.org/wiki/Denial_of_the_Holodomor
“Denial of the Holodomor is the assertion that the 1932–1933 Holodomor, a man-made[1] famine in Soviet Ukraine,[2] did not occur[3][4][5][6] or diminishing the scale and significance of the famine.[7] This denial and suppression of information about the famine was made in official Soviet propaganda from the very beginning until the 1980s. It was supported by some Western journalists and intellectuals.[4][8][9][10] It was echoed at the time of the famine by some prominent Western journalists, including Walter Duranty and Louis Fischer. The denial of the man-made famine was a highly successful and well orchestrated disinformation campaign by the Soviet government.[3][4][5] According to Robert Conquest, it was the first major instance of Soviet authorities adopting the Big Lie propaganda technique to sway world opinion, to be followed by similar campaigns over the Moscow Trials and denial of the Gulag labor camp system.[11]…………”
Yes, I’m well aware. It’s also not what I’m doing.
The official denialist propaganda generally revolves around saying it was just another natural famine and the USSR had nothing to with it. Whereas I’m saying they very much had a major role in it. Davies and Wheatcroft’s The Years of Hunger: Soviet Agriculture, 1931–1933 identifies multiple factors that led to the famine, one of which is the forced collectivization. But this was being done all across the fertile regions of the Soviet Union, all of which suffered some degree of famine. There was no deliberate singling out of Ukraine.
Why did Stalin exterminate the Ukrainians?
https://day.kyiv.ua/en/article/history-and-i/why-did-stalin-exterminate-ukrainians
“In 1933 people starved to death in many regions, but a man-made famine, with an astounding number of victims, was observed only in two political- administrative formations, where Ukrainians made up more than two-thirds of the general population: the USSR and the Kuban district of the Northern Caucasus Territory.”
In his Aug. 11, 1932, letter to Lazar Kaganovich, Stalin expressed profound outrage over the fact that dozens of raion (administrative division) party committees in Kyiv and Dnipropetrovsk oblasts dared to say that the grain procurement plan was unrealistic. He wrote, “Unless we immediately start to improve the situation in Ukraine, we might lose Ukraine. Mind you, that Pilsudski is not sleeping, and his agents in Ukraine are many times stronger than Redens or Kosior might think. Also keep in mind that the ranks of the Ukrainian Communist Party (500,000 members, ha-ha) have quite a few (yes, quite a few!) rotten elements, conscious and unconscious followers of Petliura, and, finally, direct agents of Pilsudski. As soon as matters take a turn for the worse, these elements will rush to open the front inside (and outside) of the party, against the party. The worst thing is that the Ukrainian leadership is blind to these dangers. This can no longer continue.”
I’m not interested in Ukrainian claims, since they have a vested interest in presenting the famine in Ukraine as a targeted genocide.
The first paragraph is simply a lie, since the famines in all regions of the Soviet Union in 1932-33 were partially man-made. You can’t just assert that the ones hitting Ukraine were unique; all of the Soviet farming regions were subjected to the same collectivization.
The second paragraph is supposed to prove what, exactly? All I see is a dictator mad that his underlings are sending back information that undermines his ambitious plan for rapid industrialization. If anything it could be interpreted that he’s saying that the situation of famine needs to be addressed.
Robert Conquest estimated at least 7 million peasants’ deaths from hunger in the European part of the Soviet Union in 1932–33 (5 million in Ukraine, 1 million in the North Caucasus, and 1 million elsewhere), and an additional 1 million deaths from hunger as a result of collectivization in Kazakh ASSR.
The Harvest of Sorrow: Soviet Collectivization and the Terror-Famine
https://www.amazon.com/Harvest-Sorrow-Soviet-Collectivization-Terror-Famine/dp/0195051807
The 1932 letter, from Stalin to Lazar Kaganovich is chilling.
https://en.wikipedia.org/wiki/Lazar_Kaganovich
“In all Party conferences of the later 1930s, Kaganovich made speeches demanding increased efforts in the search for and prosecution of “foreign spies” and “saboteurs”. For his ruthlessness in the execution of Stalin’s orders, he was nicknamed “Iron Lazar”. During the period of the Great Terror, starting in 1936, Kaganovich’s signature appears on 188 out of 357 documented execution lists.”
Conquest simply isn’t a reliable source.
Regardless, as someone else already pointed out, even Conquest doesn’t think there was a targeted genocide.
Cough … I’ve pointed this out long ago ….
Lysenkoism (Russian: Лысе́нковщина, tr. Lysenkovshchina) was a political campaign conducted by Trofim Lysenko, his followers and Soviet authorities against genetics and science-based agriculture. Lysenko served as the director of the Soviet Union’s Lenin All-Union Academy of Agricultural Sciences. Lysenkoism began in the late 1920s and formally ended in 1964.
The pseudo-scientific ideas of Lysenkoism assumed the heritability of acquired characteristics (Lamarckism).[1] Lysenko’s theory rejected Mendelian inheritance and the concept of the “gene”; it departed from Darwinian evolutionary theory by rejecting natural selection.[2] Proponents falsely claimed to have discovered, among many other things, that rye could transform into wheat and wheat into barley, that weeds could spontaneously transmute into food grains, and that “natural cooperation” was observed in nature as opposed to “natural selection”.[2] Lysenkoism promised extraordinary advances in breeding and in agriculture that never came about.
https://en.wikipedia.org/wiki/Lysenkoism
Robert Conquest, a great defender of Ukrainian national aspirations, was not as quite definite as one might expect about whether the Ukraine famine constituted a deliberate act of “genocide” perpetrated by Stalin against Ukrainian farmers, as some nationalists noroutinely assert.
As “the genocide became ever more firmly embedded as the cornerstone of contemporary Ukraine’s national identity, Conquest seemed to back off. ‘I don’t think the word “genocide” as such is a very useful one,’ he said to Radio Free Europe’s Ukrainian correspondent in 2006. ‘What I say is if you want to use it you can, but it was invented for rather different purposes.’ Later in the same interview he noted that ‘Andrei Sakharov said that Stalin was anti-Ukrainian, and other people have said the same. But he was anti-Ukrainian because they gave him trouble. He was also anti a lot of other people.’ Three years earlier, Conquest had told the demographic historian Stephen Wheatcroft – co-author with Robert Davies of Years of Hunger, a study of Soviet agriculture in the famine era – that it was not his opinion that ‘Stalin purposely inflicted the 1933 famine. No. What I argue is that with resulting famine imminent, he could have prevented it, but put “Soviet interest” other than feeding the starving first – thus consciously abetting it.’” —
Sheila Fitzpatrick, ‘People and Martians”, a review of two books about the Soviet famines of the 1930s, London Review of Books, Jan. 29, 2019 https://www.lrb.co.uk/v41/n02/sheila-fitzpatrick/people-and-martians
Gareth Jones was a Welsh journalist. He was murdered in 1935, most likely as another (one of millions) victim of Stalin’s NKVD. A riveting and meaningful, 29 years of life!
Gareth Richard Vaughan Jones, Hero of Ukraine
(1905 -1935)
https://www.garethjones.org/index.htm
“In the train a Communist denied, to me, that there was a famine. I flung a crust of bread which I had been eating from my own supply into a spittoon. A peasant fellow-passenger fished it out and ravenously ate it. I threw an orange peel into the spittoon and the peasant again grabbed it and devoured it. The Communist subsided…..
“‘We are waiting for death” was my welcome, but see, we still, have our cattle fodder. Go farther south. There they have nothing. Many houses are empty of people already dead,’ they cried.
A foreign expert returning from Kazakstan told me that 1,000,000 out of 5,000,000 there have died of hunger. I can believe it. After Stalin, the most hated man in Russia is Bernard Shaw, among those who read his glowing descriptions of plentiful food in their starving land.…..”
Gareth Jones (journalist)
“But they (Consulate officers) are not allowed to express their views in the press, and therefore remain silent.
Journalists, on the other hand, are allowed to write, but the censorship has turned them into masters of euphemism and understatement. Hence they give “famine” the polite name of ‘food shortage’ and ‘starving to death’ is softened down to read as ‘widespread mortality from diseases due to malnutrition’. Consuls are not so reticent in private conversation….”
https://en.wikipedia.org/wiki/Gareth_Jones_(journalist)#Life_and_career
Universities shouldn’t be in the sports business
…or debt milling.
I thought they were all over a liberal,critical thinking thing a while ago.
Extractive ontology is where it’s at.
also, taking some from the right and some from the left on unrelated issues isn’t “centrist” in most people’s understanding. Centrist implies being in the center, that is, on the same topic ending up in the middle. what the quote is describing is more properly understood as bi-modal or something like that. Not, “centrist”.
Indeed, the article describes actual centrism, in contrast to the some policies from the right and some from the left, when looking at individual issues. And unsurprisingly, those positions are supported by a majority of Americans (a different way of conceiving of centrism, i.e., majoritarianism.) But those examples are not parallel to the libertarian nirvana he asserts was once the the “center”. And notably, like centrist policies generally, they are ideologically messy. That’s because the center, in the majoritarian sense, is often supported by emotion and experience rather than ideology.
When the putative center in a democracy uses its embedded position of power to promote broadly unpopular policies that benefit its donors and to suppress popular policies that those donors oppose, you have radical centrism. It may look mild and status quo or seem like a contradiction, but the subversion of the electorate’s will in a democracy is still radicalism.
Inaction or insufficient action or opposition to necessary action in the face of catastrophic climate change is radical, endless war without any realistic exit strategy is radical, lowering tax burdens and creating tax loopholes for the wealthy and corporations in a climate of growing inequality is radical, deregulation that only the donor class want or support is radical, a system that through corruption denies the right of citizens to healthcare and bankrupts them while billionaires profit on that system is radical, privatizing social security or social benefit programs is a radical goal. Bailing out banks and not holding the people who caused the mess responsible is radical. The bipartisan center is the natural place for all such radicalism to be put into force, safe from electoral accountability. Often the worst, most radically corrupt and unpopular policies are the work of a bipartisan center that feels safe and insulated from popular repercussions. And yet all these broadly unpopular and radical policy aims are dishonestly termed “centrist”. Centrism is played in the press as if it were inherently reasonable — it isn’t — there is no rule that “centrism” cannot be radical, corrupt, or even bat s**t crazy. It often is.
In a duopoly if you pay both parties enough to support your broadly unpopular policies or to suppress broadly popular policies, the electorate is denied a say in those policies — is in fact completely locked out of the political process. Hence the “donor” part, just substitute “briber” and all becomes clear. This is common as dirt as a tactic to stymie the will of the electorate in the US two-party state. It’s not even unusual, it’s just normal everyday political reality. Of course neoliberal centrism is ideologically inconsistent, it’s simply an ad hoc shopping list for buying politicians and parties to benefit the bribe-givers by those with the means to, not an ideologically coherent political doctrine.
Like Google, Facebook is shooting fish in a barrel when it comes to advertising. Facebook can make things more private or alter the News Feed, but as long as FB knows what likes you have then it can match advertisers with those likes and sell you stuff. I’d say that’s why the stock price didn’t move. Analysts may have been assured that the ad money will keep rolling in.
Credit Karma, for instance, knows your SSN, birth date, and credit score, but it doesn’t to my knowledge really share that data. It finds financial partners to serve up offers to certain “segments” of people based on credit scores and other metrics. The people remain anonymous, but FB could tell an advertiser how many people are available in a segment.
Sherrod Brown’s not running in 2020.
A real downer for us quiz show fans: ‘Jeopardy!’ Host Alex Trebek Diagnosed With Stage 4 Pancreatic Cancer – Variety
Just got done watching the first Team Tournament of Champions last night, a weeklong affair, and he seemed perfectly fine, for whatever that’s worth in the context of “the miracle of television”. (And in said ToC, all-time-$-winner Brad Rutter beat 74-games-in-a-row-winner Ken Jennings – this time via their respective teams – yet again. At the opening of the tournament, Alex asked each team captain what he or she would do with their share of the million-dollar prize should their team win the tourney. Brad: “I’d use the money to finally visit Australia.” Alex: “But surely you don’t need that kind of money just to visit Australia.” Brad: “You do for the way *I* want to visit Australia.”)
I was a contestant and Alex was very cordial and real in person, he even ad-libbed a quip when he introduced me that was actually quite funny.
I ran into a contestant who taught college-level Shakespeare however and he completely ran the “Shakespeare” category (“Who is Horatio?” ding ding ding)
A friend of my mother’s was on Jeopardy and won something like seventy thousand dollars. She — of course I guess — enjoyed being a contestant.
Pancreatic cancer is real sneaky — many, if not most don’t notice symptoms of any significance until it’s too late
The Charlottesville news is a little odd framing… the city has already changed radically in the past 30 years as the university has grown. Even over the past 5-10 years it has changed to the point of being unrecognizable in parts (Rio road / route 29 area, downtown mall, new hotels and student housing between downtown and the corner).
The loss of the main street arena is a bummer, but it’s hard to say whether or not it will be a net positive or negative right now, and I imagine lots of the things that give it its charm (the university, great food and music scenes) won’t be impacted.
Re. Tech: “Zuckerberg says Facebook’s future is going big on private chats” [Reuters] — How much do you want to bet that FB ends up getting busted for ‘enhancing’ said ‘private chat’ feature with a keystroke logger, which bypasses the much-ballyhooed encryption? I mean, this *is* Facebook we’re talking about here – these folks just can’t help themselves.
It’ll be fine. Friends in high places, to mutual benefit.
Re: The DCCC is still at it (Twitter ad of poll omitting Bernie):
That was going around social media and the explanation was that the poll was created before Sanders announced his candidacy. I think that is awfully convenient at best, but that is the only defense offered.
I think a big reason Bernie drives Hillaryland so bonkers is he won’t engage them. He just keeps playing his game. They are trying to get him to play their game. He won’t do it
Bonkers…
Given how strongly Sanders reacted to the question of seeking advice from Hillary, when policy-wise and public deed-wise, Obama should be avoided as much, though Sanders hadn’t openly come and said so, I feel the difference in the two reactions can be traced to Hillary driving Sanders bonkers, and thus the emotional and not very rational difference.
It looks to my like Bernie doesn’t waste too much time worrying about Hillary.
He did not let that one go by quitely, though.
And, just to be safe, she should be on his mind. Watch carefullly, which he probably has done, just to make sure 2016 doesn’t happen again.
nobody tell the DCCC about the Streisand Effect. They discredit themselves better than any analysis or takedown ever could.
How does CNN cover a campaign between Trump and Sanders, when the supporters of BOTH candidates think the news is fake? :)
That is politics now. Getting office to make money by corrupt means and not to get power to make changes.
Unless you’re a Republican. Those people make changes when in power.
Yes, they are more proactive, ruthless, and less concerned about the optics in getting the money; a Democrat is more likely to be on retainer to the Finance and Tech Elites while paying more attention to the appearance of being for the people.
Think of Hillary Clinton’s very remunerative “payments” for her speeches at gatherings of Financial elites. At these speeches she said that her speeches to the masses were mendacious pablum especially anything about reforming Big Finance. (That is not a direct quote just a synopsis.)
The end results are the same though.
Getting office to make money by corrupt means and not to get power to make changes.
…otherwise known as the “Obama Method”
“Bill and Hillary Clinton don’t believe Sanders can beat Trump
So this is basically an endorsement of Sanders? Based on the Clintons track record, I can’t find another logical explanation.
I’m not sure I believe it either. After all he’s polling below Biden. But we shall see.
The thing about Facebook and private messages is about their wanting to collect metadata. Remember the social graph? They get an even more valuable graph of people trying to talk to each other privacy. One can always websearch the phrase “we kill people based on metadata”, or Snowden explaining that metadata is much more valuable than call content (because people lie in phone calls all the time, but metadata does not lie).
Give this person a Prize. Nailed it. Thank you.
Re: AOC Campaign funds:
Ryan Grim thought he had the campaign nailed on this, then looked into it further, and found this,
https://www.washingtonexaminer.com/politics/ocasio-cortezs-chief-of-staff-ran-1m-slush-fund-by-diverting-campaign-cash-to-his-own-companies
The hoops campaigns must jump through is mind boggling, as you will realize if you can make it through the whole explanation. Old saying, if you want somebody to do something (like run for office without lots of $$) make it simple. Seems like we’re supposed to pay somebody for every tiny step of the way.
“yes, this is a feature, not a bug.” – political consultant class
The AIPAC Benjamin’s, err I mean hazing, still worked. It’s amazing how fast Congress can do something when they want.
https://www.bloomberg.com/news/articles/2019-03-07/house-adopts-anti-hate-measure-in-bid-to-calm-omar-controversy
The resolution, adopted 407-23
Perhaps this is the best way to handle it.
If Omar says something similiar again, about allegiance for the second time, will it be OK, since the first time was not a problem, or will it not be (and therefore, she will not say something like that in the future)?
Personally, with this behind the Democrats, I hope she has learned a lesson and will not repeat, but will be more specific about any criticism.
The last quote which sparked this all up again:
@IlhanMN’s actual quote: “I should not be expected to have allegiance/pledge support to a foreign country in order to serve my country in Congress.”
I’d like to know how much more specific one could get…
This is interesting.
The Bloomberg article you linked has this:
Now, you write, ‘the last quote which sparked this all up again,’ quoting something not qyite the same, are you saying this is a different and later quote?
I have seen the Bloomberg quote elsewhere as well. And that is the one I have been basing my comments on. Is it not accurate (you linked the article in the original comment at 6:25pm without challenging it), or is it, as I mentioned, a second quote?
Even this quote is not specific, in my opinion. Who is she talking about expecting allegiance to a foreign country? She specifically said she, herself, should not be expected. Ok. But who is she talking about expecting that? And exactly what was involved in another person (in or out of Congress, though she is in) having allegiance to a foreign country, what did that person do?
Maybe it’s only because I had just written a rant email regarding the event here in Texas, but it was my impression that the ‘foreign allegiance’ comment by Omar was referencing the Texas speech pathologist who refused to sign an oath to not boycott Israel.
https://www.nytimes.com/2018/12/19/us/speech-pathologist-texas-israel-oath.html
Just gonna leave these 2 things here…
“You see this napkin? In 24 hours, we could have the signatures of 70 Senators on this napkin.” –Former AIPAC official Steven Rosen, speaking to a sympathetic journalist (Jeffrey Goldberg).
Israel Lobby Rebuts Omar’s Claims About Exerting Its Immense Influence By Exerting Its Immense Influence
I’m sure Johnstone is just a huge anti-semite and this will go away soon.
Millionaires and Corporate Giants Escaped IRS Audits in FY 2018
The bipartisan starving of the IRS over many years doesn’t change the fact that the last two years have been particularly bad.
The professional class hates Sanders — and they are the base of the Democrat Party.
This is a typical macro-economic overstatement. Nearly all my colleagues love Sanders and we are mostly physicians, psychologists, psychiatrists, and university profs – all with doctorates (i.e., professional class). I have not bothered to ask around about donations – not polite. I sent Bern a nice check. Oh, and I am not a registered Democrat because they are currently led by scoundrels. I vote for the candidate who comes closest to my liberal worldview. At 71, I would just once like to vote FOR a candidate rather than pick the lesser or two kakistocrats – or worse – two evils.
Do what my grandfather who died in 2004 told me:
“I wait and see which one looks, sounds, and smells most like Franklin Roosevelt, and that’s who I vote for.”
Escaping the dust bowl, starvation, and Japanese submarines in the first 20 years of your life, all of which are trying to kill you, makes you remember when someone actually tries to fix your problems
Food prices are going up fast. Until a year or so ago, a big generic cardboard tube of oatmeal was $2.49 at Safeway. Then last year it went to $2.99. Today it was $3.49. As I walked by a guy in the store I heard him say to himself “this is too much” and saw him put something back. I looked back at him furtively and he looked upper middle class (this is a rich area in CA). This is not going to work out well for people with regular incomes.
The same thing is happening in the not so rich areas of the country.
This is going to adversely affect those with irregular incomes catastrophically.
I am seeing an uptick in begging lately. I can’t blame it all on winter migrants. This wave is highly visible, while previous ‘waves’ were somewhat obscure.
Being now a “ward of the State” through the Social Security system, I experience the ill effects of the ‘chained CPI’ on standard of living levels ‘personally.’
Utilities are increasing in cost measurably in excess of increases in income as well.
gas has gone up here. i expect to be working pretty much my entire life.
I expected to do the same until ‘work’ that would have me disappeared.
The building trades are now catastrophically corrupt. The race to the bottom for wages has hit the bottom and broken through to the downside.
One aspect of the labour struggles of the turn of the twentieth century that is studiously ignored is the phenomenon of the dynamite campaigns against militant anti-union companies. This generally happened before the First World War. The literal shooting wars between the unions and the paramilitaries working for the big owner class have also been marginalized in our recollection of history. Something similar will probably have to happen again to fully resurrect the union movement in America. Whoever is coordinating the Homeland Security instrumentality probably has read this history and is planning accordingly. I can accept that the militarization of the domestic police forces is not an out and out conspiracy, but I can well believe that whatever ‘organic’ movement towards the Police State that does exist is being nurtured along by ‘interested parties.’
I’m reminded of the apocryphal story of the statesman who was talking to a member of a revolutionary party.
“What you are doing is treason.”
“Not if we win it’s not.
i’m sure that some people among tptb are planning for whatever apocalypse is shuffling toward us with the kind of nurturing you suggest. there really doesn’t seem to be any place to move to, and even survival may be something of a crapshoot. fortunately i’m old.
I’m getting old myself.
I wonder if there is any truth to the stories about older people ceding spots on the Titanic lifeboats to youngsters? I hope there is.
That graphic from Bloomberg doesn’t look like the Knight Frank report list to me.
Los Angeles and Hong Kong are missing is the most obvious thing. A couple of years ago in money magazine they had a list which said Harris County (Houston) had more millionaires that San Francisco + San Mateo + Santa Clara combined. No idea how they assemble those stats and of course a mere million is nothing like it used to be.
I wonder if London looks so hot if you remove all the Arab sheiks and Russian oligarchs. Perhaps it is just the internet ghettos I habituate (present host excluded from that description!) but the message I get is a lot of the London stats are inflated by being the favorite location for foreign pirates to stash their booty.
“The Spider’s Web: Britain’s Second Empire” is available to watch free on youtube. It’s got the goods on who they are and how they get away with it all.
A couple of things by John Prine:
Ain’t Hurtin’ Nobody (1995) live
https://hooktube.com/watch?v=bgkos1JU_wA
Great Rain (1991?)
https://hooktube.com/watch?v=0K1ukcUJ_Zg
In regards to some posts above: I’ve grown to like the 21st century ‘phone-culture’
There are two massive positives to it.
1. You know instantly, visually, who allllll the people are who you wouldn’t want to interact with/know. Looking at their phone constantly? Not a quality person you’d be interested in.
2. These people will never interrupt you for an inane conversation about the weather, or the bus schedule, or the always popular ‘how ’bout them -insert sports team-‘ conversations people seem to want to engage in.
Both ensure you won’t waste your time with, or be bothered by, people you have no wish to interact with.
I left a comment mentioning a few New York and New England seed companies that I can remember along with their websites . . . on the most recent post in the named Permaculture topic. That way, if people “remember” about it at some future time and want to find it, they will only have to read all the “Permaculture” post-category threads starting from the most recent and they will run across it. Here is the link to the thread.
https://www.nakedcapitalism.com/2019/02/new-review-dozens-studies-insect-population-decline-causes-things-can.html#comment-3114873
Since we don’t have a “survivalism” topic-category or a “jackpot readiness” topic-category to focus our offerings of “survival” information on, “Permaculture” seemed the most logical topic-category to leave this comment on in hopes it might later be found with only a semi-brutal search. If others agree with that logic, they might also offer actionable survival information on whatever is “the most recent” Permaculture post-thread at the time of their seeking to offer the information.
Good idea.
Thanks for that link, dw. This bad gardener is going to keep at it. ;)
Every one of us who is now alive is descended from a line of foodgetters who were successful enough at foodgetting to keep having offspring who kept reproducing down into our own lifetime. So an at-the-very-least minimal garden potential can be realized by almost anyone with enough informed work of the right kind.
Good enough is good enough.