We’ve been astonished at the continued poor reporting on the overhyped mortgage putback possible future action by Pimco, the Fed, Blackrock and others against Bank of America. Everyone seems so mesmerized by the names and the incorrect dollar size attached (the possible action relates to $47 billion of bonds, but the potential liability is much less; we penciled it out as at best $1 billion, and banking expert Chris Whalen concurred with our generally dim view of this suit).
The latest development confirms our dim view of this maybe-someday-will-be-a-case.
Let’s be clear: we are fans of sound litigation against banks. We are not fans of weak cases (and in this instance, not even yet lawsuits) being touted as asteroid-hitting-the-TARP-banks level events. First, it tends to lead possible litigants to pursue copy cat cases when they may have much better grounds for seeking redress. Second, when these cases either fizzle or drag on forever, it leads third parties to take all suits against banks less seriously, when some are on much more solid grounds.
So why is this not-even-a-case getting such undeserved attention? Remember, all putbacks are not created equal. Fannie and Freddie deals have strong putback rights written into them. The major mortgage lenders are all facing meaningful ongoing putbacks from the GSEs. So some putbacks are real and are imposing real costs on the banks. But it’s a big mistake to generalize from GSE putbacks to those under so-called “private label”, or non-GSE, deals.
The putback frenzy stems from the ought-to-be-dead monolines (remember them?) touting putback recoveries as their possible salvation. Many have booked large, as in wildly unrealistic, recoveries on their book. Those very optimistic recovery figures are the ONLY thing standing between them and being wound down. Law firms have been on conference calls with investors trying to stir interest. Hedge fund manager Mahal Mehta promoted the notion that this type of litigation has the potential to do a great deal of damage; cooler heads have deemed his claims to be sensationalistic and unsubstantiated.
But just as first impressions of people tend to stick, so to do first impressions of news stories. An important development on Friday, the release of a letter by Bank of America’s outside law firm, Wachtell Lipton, gave reason to think this threat of action might never grow up to be a real case. Yet this forceful retort received no where near the attention that the release of the initial letter did, garnering only a a short mention in the New York Times’ Dealbook (although it did provide the full text) and perfunctory coverage in Bloomberg.
Among other things, the missive took the unusual step of taking direct aim at the attorney responsible for this initiative, Kathy Patrick (“This and other troubling aspects of your letter strongly suggest it was written for an improper purpose, or to further an ulterior agenda”). She launched similar demand letter to Bank of New York, the trustee on $26 billion of Countrywide bonds. Bank of New York chose simply to ignore it and her move was deemed to be inept procedurally. (Many believe that the current letter, where the names of the investors were made public, is a reframed version of the failed BoNY effort).
The Wachtell letter makes clear that Banks of America is not lifting a finger until Patrick establishes the bona fides of her October request:
Please provide the following information for each of the 115 trusts listed in Exhibit A:
1. Identification of the specific provisions of the PSA for that Trust that were allegedly breached by Countrywide HLS.
2. Specify the factual basis for each allegation of failure to perform with respect to that Trust.
3. Identification of which Holders listed in your letter are claimed to be at least 25% holders of the Voting Rights in that Trust
4. For each Holder identified in Request No. 3: the class, certificate number, denomination, registered owner, acquisition date, and purchase price for each Certificate evidencing that Holder’s Voting Rights in that Trust.
5. For each Holder identified in Request No 3 that you claim to represent: (i) the names of the individuals who authorized the Holder’s signature on the letter, (ii), whether each Holder’s board of directors (or equivalent body) authorized the letter, and (iii) whether any controlling owner(s) of the Holder authorized the letter, and if so, the identities of the individuals who gave such authorization
Given the insinuations in the letter, and he request for proof of authorization, it appears likely that the letter is challenging whether Patrick and the New York Fed’s asset manager Blackrock, went through the proper steps to get approval from the New York Fed. Tom Adams prepared a spreadsheet of Countrywide bonds (see here for more detail) in the three Fed bailout entities managed by Blackrock, MaidenLane I, II (from Bear), and III (AIG CDOs, which may be germane if any of the CDOs are being liquidated).
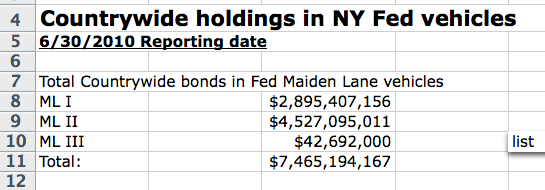Note that the total par amount of Fed bonds is $7.465 billion. Note the investor group represents $16.5 billion of bonds out out of the widely reported $47 billion, which we believe to represent face amount (the reason for referencing dollar value would be to establish meeting the 25% ownership threshold, which would be based on par value, not on purchase value). That is roughly 35% of the total. Deduct $7.465 billion, and you only have 19%, far short of the needed 25%. However, there are more than 115 issues listed on the spreadsheet (recall that the putback effort involves 115 trusts), so not all of the Fed’s deals are included in this saber-rattlings exercise, presumably because the investors collectively didn’t meet the 25% threshold. Regardless, it appears likely that the Fed inclusions was essential for at least some, perhaps a large portion, for the joint investor holdings in those 115 trusts to reach the 25% level.
MBSGuy weighed in via e-mail:
Has BofA’s law firm exposed the flaws in the investors’ demand that Countrywide repurchase billions of bad loans already?
An attorney named Kathy Patrick sent a letter to Countrywide, as servicer for billions of mortgages backing various MBS bonds, demanding that Countrywide put the loans back to the seller and alleging that Countrywide was failing as a servicer.
Ms. Patrick, thanks in large part to the impressive roster of investors, including Pimco, BlackRock (on behalf of the NY Fed), Met Life and Freddie Mac, generated a tremendous amount of media attention from her demand letter and for two weeks everyone was talking about the billions of potential exposure that banks might have due to putbacks and scrambling to understand the underlying issues and the impact on the stock prices of the banks.
The phrase “putback” is generically used to describe demands that sellers repurchase loans for purported breaches of representations and warranties made about the loans at closing. In the case of this investor group, a lawsuit has not yet been filed, but rather a demand letter was delivered as the first of several procedural steps, and challenges, the investors would have to take before they could sue the seller, or servicer. Despite the complications of such an action, and the likely years of wrangling in court, stock prices for many banks promptly dropped due to potentially adverse news, even though the outcome was far from certain. Ms. Patrick boldly proclaimed that, having served the demand letter, the clock was ticking and the servicer had 60 days before they would be held in breach of contract by the investors.
Everybody loves a good bank bashing story and this one appeared to have plenty of meat to it. So I suppose I should not be surprised that Bank of America’s response hasn’t gotten more attention. Wachtell Lipton, representing Bank of America, really rips Ms. Patrick’s letter apart. In the process, Wachtell makes a case that Ms. Patrick is in over her head and that the investor group may be getting bad advice.
I really don’t know how the Fed and Freddie got themselves involved in this, but the Wachtell attorneys are going to embarrass them at every turn. As evidence for starters, Wachtell notes the apparent irony of Freddie Mac demanding that Countrywide foreclose faster and more often when the company has publicly stated that they are “deeply committed to helping troubled homeowners keep their homes.”
The letter highlights another big issue lurking behind the potential windfall to investors in the event they are successful in forcing the seller to take back bad mortgage loans – how were investors who bought the bonds at a steep discount (Pimco comes to mind) hurt by the supposed servicing problems? The parties who were probably most damaged were who bought the bonds when they were first offered, and took the big losses. How can the Fed say it is damaged when it has repeatedly said it will make money on all of its Maiden Lane vehicles?
The Wachtell attorney effectively notifies Ms. Patrick that they clock has not started running, as she claimed when she cranked up the PR machine for her letter to Countrywide. The information requests on 115 different transactions alone could take months to put together, meaning nothing (other than a PR campaign) has started.
But then Wachtell goes on to really highlight the big issue: why was the Fed looking to sue one of its own member banks?
I am fairly certain that Wachtell would not request this if they did not already know the answer and, as a result, I suspect that they know that the board of the NY Fed did not authorize the letter. The same may apply for Freddie Mac and others in the group.
I am not a bank defender, but I really don’t like the way this whole putback issue became a sudden sensation based on such weak grounds. Given the amount of publicity the Countrywide case generated for BofA and all of the banks, one wonders if someone playing a game with this issue or trying to gain some advantage in bank stock prices?
The banks should be held accountable for the things they failed to do in the mortgage business and the fact that they are able to escape liability for the obvious and complete failure in their underwriting of mortgage loans is hugely problematic. There is no way any investor is going to come back to the mortgage market with the risk they are being asked to take, while at such an enormous information disadvantage compared to the banks.
As we indicated, this threat-to-launch-a-case was never a slam dunk, and it looks less so by the day.
38 comments
Comments are closed.
Remember the tale of the Great Oompa Loompa
The Great Oompa Loompa stood before the masses and spoke “Behold the Oompa Loompa Empire that I have built. Behold the sweet smell of success. Our stuff don’t stink!”
Then the Oompa Loompa turned to his inner council and said ” What is this crap? We’ve got seconds for 80/20’s with FICO’s under 600! I wouldn’t approve that kind of loan for my own MOTHER!, a Congressman maybe, but NOT my mother.”
Councilor Sambol replied “Sire, It is the ‘Milk’ of the Biz”
Oompa Loompa said “Milk my @%$. It’s poison! We gotta dump this stuff fast.”
Then Councilor Sieraki said ” We must match what is offered by others or the empire will shrink” and Councilor Sambol said ” Tis true”
The Oompa Loompa said ” Well be more careful, and by the way, those pick-pays stink too!”
As his councilors left the throne room, the Oompa Loompa did swear unto himself ” I will steadily sell my stake in this idiot empire and stand ready to move to the Caymans where my awesome tan will shield me from the harsh rays of the tropic sun.
Hmmm…now where did I put Ken’s number?”
http://www.sec.gov/news/press/2009/2009-249-fact-sheet.htm
I am more than happy to be corrected if I am wrong here…. BUT hasn’t Chris Whalen strongly intimated more than once that this is going to be a debilitating problem for banks in 2011??? This piece seems to indicate serious consequences would only affect the banks way AFTER (years??) the year 2011. If so, is Mr Whalen wrong here, is Mr. Whalen recently rethinking his views, or is Mr. Whalen trying to sell a lot more books this Christmas season by adding a little more expediency/alarm to the banks’ situation on “Putbacks”???
Any “enlightenment” or correction of the above would be appreciated.
I don’t see that Wachtell’s letter amounts to anything much. From the “investor'” standpoint, not much was lost by trying the letter and the PR angle. It might have worked, meaning they might have improved their positions cheaply. The bank might have responded with better service. Maybe the folks in DC will do something favorable. That an “ulterior motive” in such a matter is somehow “improper,” now that is truly a laughable statement from an attorney and suggests that the top team at Wachtell is yet on the case. More, the detailed list of information requests suggests that a bunch of associates were sat down to write memos. The prospective litigants are all big boys and girls. More importantly, they have the wherewithal to employ some firm as big and bad as Wachtell and to bring a proper case, properly documented and so forth. If I were a shareholder in one of the megabanks implicated in the foreclosure mess, I would want my management to be considering ways to defuse this issue and not hide behind lawyer letters. It’s bad news when litigation is the cheapest solution and pre-fight warmups are even cheaper.
This part of drfrank’s comment strikes me as spot on:
“That an “ulterior motive” in such a matter is somehow “improper,” now that is truly a laughable statement from an attorney and suggests that the top team at Wachtell is yet on the case. More, the detailed list of information requests suggests that a bunch of associates were sat down to write memos.”
Wachtell is just woofing. Their demands for verification are nothing more than a dress rehearsal for formal discovery. They can get their formal discovery, AFTER their clients are sued. Ad hominem attacks in such Wachtell’s letter do NOT equal “truth” and do NOT form the basis for slandering the skill or competence of the investors’ attorney.
Fractal,
It’s very unusual for a law firm to attack another attorney personally, particularly in a letter signed by more than one firm (Goodwin Proctor and Munger Tolles also signed the letter). This was not done casually or without having a lot of eyes on the text, as your comment about associates implies.
In addition, Wachtell has a close relationship with JP Morgan. Jamie Dimon is an A class director of the New York Fed. There are decent odds that Wachtell put a query into Dimon as to whether the NY Fed board was briefed on this and approved it. So their allegation about lack of proper approvals may be far from mere “woofing”.
The litigation is important and it may become significant, but mostly the PMI litigation in my view. Get a decision against BAC by MBI and then life gets interesting. No longer bankruptcy remote IMHO.
The RMBS investors have little real leverage here, even if they get 25% of holders. Then BAC says GFYM and see you in court. Take a number. Listen to the BAC CC re: ramping servicing capacity. Tranche warfare me thinks. .
There are four significant things that could kill BAC and mortgage reps & warranties claims are just one of these. Stay tuned.
http://www.rcwhalen.com/pdf/Darden_102910.pdf
Chris
I’m sorry, can you repeat that part about 2011 again???? I think I missed it AGAIN.
This probably isn’t the blog for this type of thing, but I say fuck the investors. Homeownership is more important. Wealthy investors are part of the snot-rich class, who don’t really do hard work (but insist they do), money flying all over the place, they throw money at big law firms to come up with wordsmithed, semantic bloviations to serve their causes. There is real pain all over the world and you have these well cushioned son’s of bitches determining who lives, dies, will be homeless, will be in jail, which countries will be attacked and so on – it’s just evil. In just boggles the mind how the grifter class assumes they are bound by law, order and rules. That’s bullshit.
I hear BofA is in discussions with the Fed about a bigger problem as we speak.
As for the legal grandstanding on both sides on the putbacks, the Fed’s involvement in the case is meant to signal to BofA that the Fed is willing to make things uncomfortable to BofA. The Wachtell response tho, is not so much directed at the Fed as at BofA shareholders.
Another thing to consider is that we know terms of the PSA’a were regularly violated. ( I challenge readers to post evidence of documentation on a single Countrywide or Aurora mortgage originated in a mid-2000’s year, that was put into the trust on time, and that went through the true terms stated in the PSA’s — not the loophole listed in the PSA’s that says they can do anything they want if it was industry standard or validated by their accountants. The have some more fun trying to trace it back out of the trust into a foreclosure proceeding.) The potential liability from this is tremendous. The putback suit is a sideshow. So, what does the Fed want from BofA? Is serious mortgage mods and some punitive cramdowns concessions, enough?
The Fed’s plan to release criteria for banks to issue dividends or engage in buybacks, gives us the answer. The release of the criteria now is designed to be a defacto STRESS TEST. Investors will reward those banks that pass and hurt those who fail. We know that Wells Fargo and JPM Chase have indicated they will pass. Which banks will not? Don’t get caught up in the seemingly amateurish suit and Wachtel’s frat boy response. it is part of a bigger game being played right now that you should be watching out for.
With all due respect, I’ve spend a good deal of time with attorneys who know this area of litigation intimately (as in knowledge of rep and warranty cases over the last 20 years, plus up to speed on the state of play in structured credit litigation). They are NOT bank friendly, quite the reverse, but they regard this effort as weak, with the potential to undermine the perception of much more solid cases against banks).
To prove damages, you need to show that the reps and warranties were breached (the point you make) AND that THAT was the reason the loan went bad. The latter part of the proof is very costly and difficult.
You also assume the Fed approved this letter. The last move by this lawyer was done without revealing client names. Blackrock may have given the go-ahead for this letter as the Fed’s asset manager, with a plan to get Fed approval for the actual litigation. Revealing the text of the letter was not likely to have been authorized by the clients, and if so, this suggests the lawyer is a loose canon, perhaps a bit desperate.
Please read my posts on this, we might then have a better discussion.
http://www.nakedcapitalism.com/2010/10/pimco-ny-fed-pressuring-bofa-to-repurchase-dud-mortgages-empty-threats-edition.html
http://www.nakedcapitalism.com/2010/10/more-on-why-the-pimco-blackrock-freddie-ny-fed-letter-to-countrywide-on-putbacks-is-way-overhyped.html
http://www.nakedcapitalism.com/2010/10/more-on-the-peculiar-pimco-blackrock-new-york-fed-putback-letter-to-countrywide.html
Yves, there is no basis in what you reported so far in this diary for this slander: “Revealing the text of the letter was not likely to have been authorized by the clients, and if so, this suggests the lawyer is a loose canon, perhaps a bit desperate.”
If there are public relations tactics that you approve or disapprove of, certainly say so. But you are accusing investors’ counsel of incompetence, based solely on PR tactics, not on the merits of her demand for putbacks. That oversteps the proof you have offered so far.
You acknowledge you have anti-bank lawyers among your sources who are dubious of the strength of this particular putback demand: “They are NOT bank friendly, quite the reverse, but they regard this effort as weak, with the potential to undermine the perception of much more solid cases against banks).” But those sources say nothing about the competence of investors’ counsel, merely that the case may be “weak.” If they have stronger cases, or if they have more aggressive PR tactics you would approve of, let them step up and show their hand. Meanwhile, it is a mistake for you to slander investors’ counsel because it distracts from the critical issue: the terms of the PSAs.
Fractal,
First, every attorney I have spoken to (and they are on the side that sues banks) all regard Patrick’s move of publishing the letter (and she did so, this was not a leak of some sort) as extremely unusual, so much so that they all questioned how it came about. The normal way to expose a letter like this is for one of the clients to present or simply to leak it.
Second, her procedural moves on the first action, the trustee case, were inept. There is no nicer word for it. She has scored successes on M&A related litigation, but this is a different ballpark. So she has just had a highly visible professional flop. And I did mention that in the post. So there is reason to question her sophistication in this particular arena, and not just what appears to be an awfully aggressive press strategy.
Third, Patrick’s press moves (and the communication with the media has all been by Patrick) look like grandstanding. To talk about billions of dollars of damages when you haven’t even passed the procedural hurdles to file a claim? And this is an area where the claims, even when they are made, can and often do drag out a long time. This is not the conduct one normally sees from a professional dealing in large corporate matters (good client management is to underpromise and overdeliver; her remarks about this matter, which isn’t even a case yet, amount to overpromising in a very visible way). She’s been unusually chatty with the media for a lawyer pursuing even a real case, and this is a wanna-be case. And the was a profile on her in Bloomberg just after she publicized the letter that looked very much as if a publicist were behind it.
Fourth, my comments were written. Comments that are not factual and are damaging is libel, not slander. But my remarks have factual support that you have not considered.
Fifth, the real issue is that investors are finding out that their ability to get recourse in these deals is crappy. Rep and warranty breaches ought to be a serious matter, whether or not they result in harm. I’m being shot as the messenger in saying that the banks who clearly DID behave badly are probably not going to suffer much (except the aggravation of the ongoing bad press and the resources needed to fight) from these rep and warranty cases.
Sixth, I HAVE discussed litigation that I think will have an impact (cases based on standing, the suits against LPS, litigation based on the broader issue of whether the mortgage loans were properly conveyed to securitization trusts, the state AG investigations). I’ve presented numerous legal theories that appear to be much sounder than this action. Asserting that I’ve been remiss in this area is way off base.
If you think having a functioning securitization market is important (and I’m skeptical that it should be anywhere near as big as it got to be), investors need much better protection. Fannie and Freddie have it, their putback process isn’t onerous. The investors in private paper got much less protection on this front and are likely to suffer the consequences.
I’m with Morning Rage. This site appears to have gone “bankster friendly” in a hurry:
“However, it seems like this approach to fighting the banks is very weak and potentially discredits other stronger arguments. It is a shame that the investors are joined together for this cause, when they could have, when united, accomplished much more if they worked to rebuild the mortgage and securitization markets and to find solutions to the foreclosure crisis that worked for homeowners and investors.”
That sure sounds like Banksters are to be let off the hook for all their crimes. In the name of expediency, TBTF style. Wall St gets a free pass, as always. Pathetic.
If those are not the views here, then you need to clarify them, a lot.
With all due respect, reread the post, and the one I linked to at the top, which discussed the $1 billion max damages.
Just because the bankers looted America does NOT mean every legal theory of action to get back at them is sound. Jumping on the bandwagon of ill conceived, weak lawsuits (and this isn’t even a lawsuit!) will deter people from spending the time and effort to pursue ones that could be big winners and hence serve as retribution for bad bank behavior. Litigation is a VERY costly and high-stakes game, and when the banks prevail, unless people understand why, it will deter lawsuits.
So I gather you’d rather have me lie and say this is a great potential lawsuit just to bank bash. That’s your message. I’ve been a continuing critic of the banks, but I believe in being truthful. My credibility as a critic rests on having sound analysis to back my negative views.
This is investors seeking to move the markets either not doing their legal homework or being utterly cynical to push bank stocks around, and on Pimco’s behalf, to potentially do a pump and dump on MBS it owns (a ton, I might add).
We’ve been hugely critical of the banks on MBS. We had an op ed just last week the NYT saying the banks needed to do serious mods, and how bad the MBS mess was about to be.
But as I discussed long form in REPEATED posts, this is a rep and warranty case. Those yield comparatively small settlements because they are very hard to prove. It isn’t merely that the bankers violated underwriting standards, you have to prove that was why the loan (and you argue loan by loan) went bad. With unemployment at 17% and the economy in the toilet, a lot of these loans will be shown to be going bad due to job losses and cutbacks in hours, not the loan being bad. In fat, most of the really bad loans went into default in the first six months after being made. Those can’t be put back, they are LONG gone.
In addition, as I stress in the post, the lawyer on this case is over her head. Everyone I know who follows this space is astounded that she got hired by this crowd. I’ve had credible people speculate that the only logic they can fathom is they (Pimco? Blackrock?) wanted this effort to fail in a visible way. That is too extreme a view for me to endorse, but the fact that savvy people are straining to come up with explanations shows how bizarre the choice of this lawyer is.
See these posts:
http://www.nakedcapitalism.com/2010/10/pimco-ny-fed-pressuring-bofa-to-repurchase-dud-mortgages-empty-threats-edition.html
http://www.nakedcapitalism.com/2010/10/more-on-why-the-pimco-blackrock-freddie-ny-fed-letter-to-countrywide-on-putbacks-is-way-overhyped.html
http://www.nakedcapitalism.com/2010/10/more-on-the-peculiar-pimco-blackrock-new-york-fed-putback-letter-to-countrywide.html
Friday afternoon announcement that FHLB will also seek $375 Billion of putbacks onto BAC.
http://www.zerohedge.com/article/bank-america-reports-no-day-trading-losses-q3-announces-mbs-complaints-over-375-billion-wort
I could see the states wanting their share of the loot as well. The banks appear to be the last man left standing with any money.
That case actually got dismissed yesterday.
http://www.sec.gov/Archives/edgar/data/70858/000119312510250276/dex991.htm
I think that’s a different case.
I am pretty sure it’s the same case. What happened was, the news of dismissal came out AFTER the 10-Q report was filed. So CNBC went with the story that BAC was facing 370 billion MBS lawsuit. I think this was a PR stunt by bank of America. They knew the case was going to be dismissed before the 10-Q filing.
Dealbook at the NY Times confirms exactly what John said above.
Sorry, I stand corrected. Strange though because the amounts are a little different as well as the plantiffs mentioned in each article.
When I first read the headline it puzzled me because I thought Bank of America already detailed their potential putback exposure and the figure seemed too high. After reading the article it seems Bank of America is one of several defendants. As Yves has been saying for a few weeks now, one really needs to be careful about these headlines. Very misleading, I think.
Sorry, this is a reply to John’s comment above.
I have no inside baseball to offer, but I’m extremely uncomfortable with a number of assumptions that run through this post and thread.
On the basis of some personal experience with the lawyers (on both sides, incidentally), I think the contempt being expressed for them is pretty silly. Wachtell is a good firm, not a bunch of frat boys, and Kathy Patrick has a pretty impressive track record. Admittedly, the choice of law firms on both sides is intriguing. Enough said about that.
I hear you on the weakness of the underlying legal theory, but have to wonder if the situation has developed far enough to have any very good idea of how far it can be taken. I’m not enough of a Machiavellian to say how the New York Fed’s involvement came to pass–though I’d note that contemporaneously with the initial announcement of the demand letter the president of that institution made a speech alluding publicly to back office weaknesses supporting the MBS markets.
If your point is simply that this dispute is being overplayed by the media and is not the stake to be driven through the vampire’s heart, you’re right, of course. But the dispute is an interesting development and probably a bit more than that. I mean, really, lawsuits against trustees in these situations usually are just a way to pressure the trustee to resign.
I’m with the guy who commented that these lawsuits are important (and when I say, ‘these lawsuits’ I’m not referring to the one contemplated by this demand letter necessarily, but to the whole unfolding universe of litigation over a variety of MBS owner/trustee/servicer/foreclosure issues).
apache,
This is not a new area of litigation. Rep and warranty cases of this sort have been around for over 15 years. This one just has more zeros attached and bigger names than most. And this isn’t litigation yet, this is just a letter! The lawyer hasn’t passed the procedural hurdles to file a claim!
They are pretty much not litigated very far because they costs are really high. And the high costs means they tend not to yield very much to the party initiating the action.
Put it this way: yesterday I ran into a lawyer from a very big investment firm at a speech I was giving and she buttonholed me as to why I wasn’t so keen about this case. As soon as she understood that these were not 1933 or 1934 act claims, but straight up contract rep and warranty breaches, I didn’t have to explain any more.
This blog’s credibility just dropped significantly in my book. Sweet shadow marketing for BOA. READ a PSA. Any PSA. Clearly breached notice provisions for bad mortgages and warranties.
AJS,
I’m just about last person who can credibly be charged with carrying the banks’ water. You are out of line in personalizing your disagreement.
And your assumption, that rep breach = succes in litigation, is incorrect. Your remark suggests that you do not understand the threshold needed to have a viable claim.
It isn’t a mere matter of having breached the agreement. You ALSO need to show that you suffered damages as a DIRECT result of the breach.
These cases are very expensive to pursue because you fight them on a loan by loan basis (even if a judge agrees a on sample, which has never happened in one of these cases yet, but at least one judge seems receptive to the notion in a current action) the conventions of how underwriting was done suggests a sample would need to be 10%. On 115 pool with a typical 5000 loans in each, 10% is 57,000 loans. The bank can and will argue that most if not all of the losses were normal credit losses: job loss, income reduction, death, disability.
In addition, the really bad loans went tits up very shortly after they were made, in the first three-six months. Given that the subprime market stopped completely in July 2007, the overwhelming majority of the very worst loans have likely been foreclosed upon already.
If you took ANY investor and asked, “Did you model for unemployment at 10% and housing prices down 25-45%” the answer is no. And if you made them run their models with those assumption, the odds are VERY high you’d see losses at least as high as you see now.
And as we indicated, which you also ignored, is that this threat has to pass some difficult procedural hurdles to even get to be a case (the monolines, who are the only ones to get to the discovery phase on real litigation, have much better claims and grounds for overcoming the procedural hurdles. Chris Whalen, who weighted in earlier in comments, also agrees here).
The real issue, which you appear unwilling to consider, ought to be, “why do such clear rep and warranty breaches make for not such hot cases?” But it appears to be more fun for you to shoot the messenger.
Yves, before you get too angry with the posters on your blog, perhaps you should consider one possibility.
Perhaps this suit which may appear ill timed and not well prepared or supported: is infact an attemp to sabotage future suits (This is vaguely hinted at by others). Such plays are certainly not unknown in law.
I know nothing about Kathy Patrick or her background. It would seem to be a very bold sensational step for an individual attourney to take on BofA in this context when the Fed is obviously loath to do the same. Perhaps a good first step in getting to the facts would be to reseach the Lady’s CV to establish motive and prospects for success.
Here in Canada we had a Prime Minister who walked free from criminal prosecution because a law enforcement official purposely leaked incriminating evidence and thereby tainted the evidence. just saying??
Yes, I know I should not get annoyed and argumentative, but is it frustrating when the people making comments appear not to have read the post. The reaction is basically “What, you are criticizing a suit against banks? How dare you!” In reality, misguided litigation only helps lawyers. And the real question ought to be “Why are these sorts of suits not so attractive, when the banks clearly DID behave really badly?”
I’ve had some professionals in the area say they are so confounded by this case that the can only surmise that it is a Trojan horse. I’m not sure I buy that, but I can see Blackrock being highly motivated to keep putting attractive marks on all the ML entities, particularly since the Fed has insisted it won’t lose money on them, and all the hype might help them in that regard.
Mr. Repstock,
I see your comment as very likely the most intelligent one in this thread. I often wondered if the same thing didn’t happen with Ted Stevens up in Alaska. The timing and situations where these things happen seems to be so coincidental. I think it should be very fascinating to watch Miss Patrick’s future career path and what things are “thrown her way” in the future. Although it sounds like a wild theory, if you look at motivating factors it is a very sound and perceptive thought on your part.
I’m too lazy to confirm this but I read in the WSJ a week or two ago that Kathy Patrick has been pretty successful in the past with cases involving significant amounts of money, and that she has a “go for broke” approach toward litigation.
YVES: There will always be some people questioning your objectivity due to their own emotional biases. The fact that you have been clearly critical of the banks in the past as well makes me feel you are one of the most objective bloggists I know. Its easy to jump on the bandwagon. But I respect your objectivity because that equals credibility.
—“…Kathy Patrick has been pretty successful in the past with cases involving significant amounts of money, and that she has a “go for broke” approach toward litigation.”—
Be that as it may Pelican; this suit would need to be well funded. I would guess that if it were ever sucessful, payout might not come for 10-20 years. Did the article mention anything about Ms. Patrick being independantly wealthy or a crusader?
Paul, I don’t remember much detail although she was known as a “pitbull”. I agree that it is an uphill battle for her.
Thanks. What I am suggesting is that a “go for broke” attitude in this case is lawyer serving, not client serving. And she appears so committed to trying to win that she is engaging in what are likely to be Hail Mary passes.
Look, she tried with her trustee action and got nowhere, no suit came out of this. She’s trying another strategy in an area new to her, and if she can’t allege specific breaches of the PSAs on the trusts, the odds are pretty decent a judge will not be sympathetic and will nix the case in the early stages (summary judgment or other procedural motion). The threat to remove the servicer, which is the one action investors might take without going to court, even if she could get enough on her side (it takes a majority or supermajority, depending on the PSA for the particular deal), is empty (that was our initial post on this topic). The investors will have to pay more to get a new servicer in, and there is no assurance it will be all that aggressive on putbacks (that simply isn’t something servicers, which are factories staffed mainly with low level workers) are set up to do.
As Chris Whalen remarked above,
The RMBS investors have little real leverage here, even if they get 25% of holders. Then BAC says GFYM and see you in court. Take a number.
“What I am suggesting is that a “go for broke” attitude in this case is lawyer serving, not client serving. And she appears so committed to trying to win that she is engaging in what are likely to be Hail Mary passes.”
***I agree completely. I was just mentioning what I read per the WSJ. This case may be her “Peter Principle” in terms of litigation, I don’t know. That said, I also thought about three things. First, maybe investors were being just as self-serving, perhaps involved in some kind of legal securities manipulation which you yourself considered. Second, I wondered about the arrangement between Kathy Patrick and the investors. Was she doing this on (partial) contingency? Not being a lawyer maybe this is a silly thought but if she were to get $1 billion in a settlement and rake in half that maybe it would still cover her costs. Or not. I don’t know. But I did ask myself what investors have to lose by not trying to get some money back as long as the amount they expect to receive is greater than the anticipated expenses. These are big dollars and even just 10% of $17b isn’t chump change in an absolute sense at least. Finally, I wondered about fiduciary duties. Would Blackrock and the NY Fed be remiss if they didn’t try to bring legal action against the banks? Anyway, I can understand why Bank of America’s lawyers are suggesting that the plantiff’s lawyer has some ulterior motive.
Yves, I have read every daily post on this Blog, and many of the links posted, for many years. I rarely comment, not enough time.
I meant no personal disrespect, you have done some great work.
With all due respect (love that phrase, it’s always used right before the sledge hammer is dropped) I have difficulty reconciling your statements in this post with support for a “Swedish style solution”.
A statement like “…if they worked to rebuild the mortgage and securitization markets and to find solutions to the foreclosure crisis that worked for homeowners and investors.” sure sounds to me like Banksters are TBTF and for the “good of the economy” etc we just have to shrug and let it go. That isn’t your intention, I know, but it sounded like it to me, at first read.
Personally, I want to see a Bankster swinging from a rope on every lamp post on Wall St. Period. I’m out for blood. The death penalty would be letting them off easy. A few years of torture would be appropriate before a public execution.
Anyway, don’t get angry over my words. When you write a Blog, people may disagree, some of them more harshly than others. I could have been more diplomatic there, but I am seriously pissed at “financial engineers”, as you can tell. I’m just a distant armchair observer, no one listens to me anyway. Keep up the good work, and don’t let my criticism get to you. I always recommend NC to everyone I meet when discussing the economy etc, but probably few read it, apathy is still rampant. Thanks for all your efforts.
1. Civil litigation like this letter which will probably never result in a suit is not going to lead to any perps hanging from trees. Even if it were to succeed, that wouldn’t happen
2. Having the media hype legal strategies that probably won’t work leads to distorted securities prices, which means this could be a pump and dump operation. So promoting weak legal actions actually helps the finance industry loot ordinary people once again
3. Promoting weak legal action encourages copy cat actions. This helps the lawyers and the banksters, since they waste time and energy on legal activity that is very unlikely to have any impact, rather than on legal theories that could really take a pound or two of flesh out of the banks.
Gents:
It appears that the BofA Comment on Court Ruling: “Bank of America Corporation today announced that on November 4, 2010, the U.S. District Court for the Central District of California granted Countrywide Financial Corporation’s (“Countrywide”) motion to dismiss the amended complaint in the putative securities class action entitled Maine State Retirement System v. Countrywide Financial Corporation, et al. (“Maine State”).” refers to a different case than the 375Billion of MBS litigation listed on pg. 60 of the Nov. 5 10Q. The current 10Q lists new litigations filed since the last 10Q. The dismissed case was filed on Nov. 4 2007, and as such was probably disclosed in 2007 or early 2008.
Note that under the paragraph for MBS litigations suing for $375B,”The Corporation has previously disclosed some of these matters under other headings, in its 2009 Annual Report on Form 10-K and Quarterly Reports on Form 10-Q for the quarters ended March 31, 2010 and June 30, 2010, including Countrywide Mortgage-Backed Securities Litigation; IndyMac Litigation; Merrill Lynch Subprime-related Matters; and Federal Home Loan Bank of Seattle Litigation.” So I can safely assume these are not the same cases. Am I correct?
That’s not the report in the NYT Dealbook. The part you are missing is that the dismissal of the $375 billion case came too late in the day for it to be removed from the current 10Q. So it is listed in the current 10Q even though it has actually been dismissed.