By Claus Bjørn Jørgensen , Sigrid Suetens, and Jean-Robert Tyran. Cross posted from VoxEU.
Japan’s trio of tsunami, earthquake, and nuclear disaster has left the world stunned. As this column points out, even the experts were shocked. But while these events were highly unlikely, they were still possible. This column uses evidence from the Danish lottery to show that people tend to adjust their expectations of future events based on only small pockets of recent experience, often at their cost.
Important events are hard to predict – a fact that is particularly hard-felt when it comes to low probability events with dramatic consequences. Nuclear catastrophe, financial crisis and the like are things that even experts struggle to predict. The difficulty stems from a lack of understanding of the underlying factors and complex interactions among causes (probabilities are not independent but conditional on other events).
Experts are thus to some extent forced to base their predictions on inference from observing the past. A difficult issue is to know when a model should be revised given that an event that has been deemed to be highly improbable happens to occur. The issue is most relevant for policy recommendations. For example, what recommendations should experts provide for the regulation of nuclear power in the wake of the Fukushima disaster or for the regulation of banks in the light of the recent financial crisis?
While experts struggle to predict such events accurately, the average person is often simply baffled. They tend to misperceive randomness in a variety of ways, especially when it comes to rare events.
One common tendency is to see patterns in random data when there are none.
This can lead to a tendency to overreact to recent events, allowing their occurrence to change beliefs about future events in exaggerated ways. More specifically, many people tend to over-infer characteristics of the underlying probability distribution when observing a small number of random events. A literature pioneered by Tversky and Kahneman (1971) has identified the belief in the “law of small numbers” as the source of such over-inference.
Why do people “over infer” from recent events?
There are two plausible but apparently contradicting intuitions about how people over-infer from observing recent events.
The “gambler’s fallacy” claims that people expect rapid reversion to the mean.
For example, upon observing three outcomes of “red” in roulette, gamblers tend to think that “black” is now due and tend to bet more on “black” (Croson and Sundali 2005).
The “hot hand fallacy” claims that upon observing an unusual streak of events, people tend to predict that the streak will continue.
The “hot hand” fallacy term originates from basketball where players who scored several times in row are believed to have a “hot hand”, i.e. are more likely to score at their next attempt (e.g. Camerer 1989).
Recent behavioural theory has proposed a foundation to reconcile the apparent contradiction between the two types of over-inference (Rabin and Vayanos 2010). The intuition behind the theory can be explained with reference to the example of roulette play.
A person believing in the “law of small numbers” thinks that small samples should “look like” the parent distribution, i.e. that the sample should be representative of the parent distribution. Thus, the person believes that out of, say, 6 spins 3 should be red and 3 should be black (ignoring green). If observed outcomes in the small sample differ from the 50:50 ratio, immediate reversal is expected. Thus, somebody observing 2 times red in 6 consecutive spins believes that black is “due” on the 3rd spin to restore the 50:50 ratio.
Now suppose such person is uncertain about the fairness of the roulette wheel. Upon observing an improbable event (6 times red in 6 spins, say), the person starts to doubt about the fairness of the roulette wheel because a long streak does not correspond to what he believes a random sequence should look like. The person then revises his model of the data generating process and starts to believe the event on streak is more likely. The upshot of the theory is that the same person may at first (when the streak is short) believe in reversion of the trend (the gambler’s fallacy) and later – when the streak is long – in continuation of the trend (the hot hand fallacy).
In recent work, we use a unique data set from lotto gambling to confront this theory with the data (Jørgensen et al. 2011). Lotto gambling provides a particularly convincing opportunity to demonstrate biases in prediction.
The underlying random process is known and every effort is made to make it transparent (the drawing of balls from an urn is aired on TV and subject to government monitoring).
It should be clear to any observer that lotto numbers are truly random, and that observing past draws provides no information whatsoever about future draws (i.e. draws are truly independent).
The data used in this study is unique because we are able to track individual lotto players over time (Clotfelder and Cook 1993, among others, have used lotto data to study the gambler’s fallacy but these researchers were not able to observe individual choices).
The ability to track individuals over time allows us to study how lotto players react to recent draws. These reactions provide a measure of how lotto players predict future draws based on past observations. We use a large data set from the Danish 7/36 state lotto to investigate whether the gambler’s fallacy and the hot hand fallacy occur in a natural but tightly controlled environment with high stakes, and whether the two biases relate as theorised.
We find evidence for both types of bias and show that the biases are indeed related as hypothesised by Rabin and Vayanos (2010). While most players tend to pick the same numbers week after week no matter what, those who do react tend to react by avoiding numbers drawn in the previous week but tend to favour numbers drawn several weeks in a row. Importantly, the individual-level data allows us to show that the two biases are systematically related. Players who are prone to the gambler’s fallacy also tend to be prone to the hot hand fallacy. While the two biases exist and coexist to some extent (i.e. some players are not prone to either bias, some are prone to only one of the biases, some to both), these biases on the individual level are sufficiently pronounced and systematic that they are also visible in aggregate data.
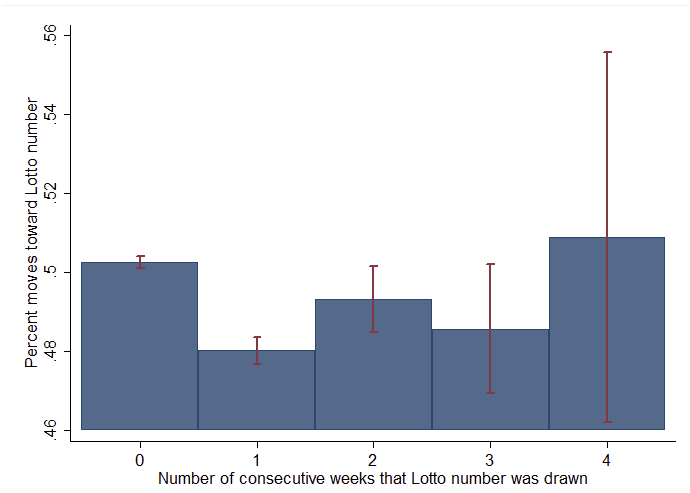
Figure 1 shows the percentage of all reactions (a move toward a lotto number that has been drawn) as a function of the number of consecutive weeks that the lotto number was drawn. For example, the first bar shows that if a particular number was not drawn in the previous week (a likely event) players are relatively indifferent about the number they pick (they are about equally likely to pick the number or not). The second bar shows that if a particular number has been drawn in the previous week it is significantly less likely to be picked (by about 2 percentage points), indicating the presence of the gambler’s fallacy at the aggregate level. The bars further to the right show that as a particular number happens to be drawn several times in a row (an unlikely event) it tends to become increasingly popular compared to the case where the number has been drawn in the previous week only. These results from lotto gambling are in line with recent findings from the experimental laboratory (Asparouhova et al. 2009).
Figure 1: Percentage of moves toward Lotto numbers as a function of number of consecutive weeks that Lotto number was drawn (including 95% confidence intervals)
Costly misperceptions
The belief that winning lotto numbers can be predicted from observing past draws may seem simply absurd, but is such a bias also costly? We find that the answer is yes, and for two reasons.
Biased players tend to lose more money.
Biased players buy systematically more tickets and — given that the payout rate is 45% in Danish lotto — buying more tickets means losing more money on average. This result suggests that players who are biased in the particular ways studied here may also misperceive the small chance of winning in the first place (the chance of winning the jackpot is about 1 in 8 million in the Danish lotto).
Biased players tend to win less.
The reason is not that biased players are less likely to win (all numbers are equally likely to win) but that biased players tend to pick the same numbers as other biased players. That is, biased players win smaller amounts given that they happen to win. Lotto has a “pari-mutuel” structure because the prize money per category is fixed and shared among the winners.
Biased players tend to pick the same numbers as other biased players, and such coordinated moves to particular numbers reduce the winnings per player. An extreme example from the Bulgarian 6/42 state lottery illustrates the point. In September 2009, the exact same six numbers were drawn in two consecutive weeks. While no player picked the winning numbers in the first draw, 18 players did in the second draw. These players then had to share the jackpot and lost about 94% of the prize money compared to the case with only one winner.
Conclusion
Using data from the particularly clear-cut case of lotto gambling, this study shows that laypeople tend to draw strong conclusions based on few observations, and that biases are common and systematic when predicting improbable events. In a more general perspective, such biases may induce public opinion and the media to call for dramatic swings in policy in response to highly improbable events. Politicians are then under pressure to yield to popular demands for drastic regulation. However, regulators would be well-advised to be aware of the common tendency to over-infer regularities from rare events and to carefully investigate whether observed data indeed warrants a dramatic swing in policy.


In a more general perspective, such biases may induce public opinion and the media to call for dramatic swings in policy in response to highly improbable events. Politicians are then under pressure to yield to popular demands for drastic regulation.
1. Politicians and media are part of the congealed elites on one side, with the people on the other.
2. I can’t think of a single example of “public opinion” pressuring those poor harried politicians into anything. On the contrary, without exception every policy I can think of was imposed by autocratic fiat, and more often than not the de facto Goebbels ministry did all it could to Shock public opinion into acquiescence if not support for these anti-public policies. Fear, hate, and confusion are systematically manufactured from the top down.
So however true the phenomena described in this post as a general feature of psychology, it’s a minor detail in the political realm. There the overwhelming phenomenon is systematic obscurantism supplemented by state terrorism and violence, not irrationality on the part of the individual.
I was with the authors up until the quote you cite. And then they lost me. This is the perfect example of where rationalism is used in an effort to trump science and democracy.
The authors pre-decide what conclusion they want—-minimal regulation—-and then cherry-pick evidence (human psychology) to substantiate their argument.
Their argument only works if you are talking about $$$$ vs. $$$$, where every $ has the same psychological worth as every other $. Also, it also works only if you can put a dollar value on everything, nothing being sacred. Both assumptions—-when we’re dealing with flesh and blood human beings and not homo economicus—-are false.
To being with, numerous empirical studies have shown that a dollar lost, when talking human psychology, is not the same as a dollar won. This is especially true when the dollar lost is needed to purchase essentials or things considered essential, like food and lodging, or a dignified retirement.
Second, for most human beings (certainly not the sociopaths that make up most of the ranks of the economics profession) there are certain things that are just sacred. They have no dollar value. These might include life and limb or health. One of my father’s favorite sayings was “the beauty of the earth and the fullness thereof.” He was quite the outdoorsman and believed that the earth and its beauty were sacred. Is this not just as much a part of human psychology as the psychological phenomenon the authors cite?
The idea that nothing is sacred and a $ value can be placed on everything is a theology that emanates from the Chicago School, most notably from Gary Becker and Richard Posner. The best reference text I’ve found on this is “Chapter 7: Chicago vs. The Ten Commandments” from Robert H. Nelson’s Economics as Religion.
Becker carries the “everything has a $ value” theology to its most extreme when he argues that “the various acts of persecution of the Jews could be condemned only if they were shown to diminish the aggregate utility of all the people in Germany.”
In Sex and Reason Posner finds that marriage belongs to the same basic economic category as prostitution. Or, as Posner explains,
In describing prostitution as a substitute for marriage in a society that has a surplus of bachelors, I may seem to be overlooking a fundamental difference: the “mercenary” character of the prostitute’s relationship with her customer. The difference is not fundamental. In a long-term relationship such as marriage, the participants can compensate each other for services performed by performing reciprocal services, so they need not bother with pricing each service, keeping books of account, and so forth. But in a spot-market relationship such as a transaction with a prostitute, arranging for reciprocal services is difficult. It is more efficient for the customer to pay in a medium [of money] that the prostitute can use to purchase services from others.
There’s much more. Criminals are distinguished not by their lack of moral character, but by the fact that “their benefits and costs differ.” In a real sense, “frauds, thefts, etc., do not involve true social costs but are simply transfers, with the loss to victims being compensated by equal gains to criminals.” The full workings of the institution of marriage can be analyzed “in the manner of a typical exchange relationship in the marketplace.” Decisions about marriage, divorce, children, and others made in families are in essence “acts of consumer choice.” The current birthrate might be seen as reflecting the intersection of a “demand curve for children and supply curve.”
Only by looking at human psychology through the lens of Becker and Posner could one come to the conclusions that the authors did.
“frauds, thefts, etc., do not involve true social costs but are simply transfers, with the loss to victims being compensated by equal gains to criminals.”
That’s certainly typical economist thinking, even if they’re usually too cowardly to phrase it that way. Indeed the criminal’s the one showing the entrepreneurial, profiteering spirit, which of course trumps everything else.
Our elites, who are certainly criminal, believe this. And since they are so much better and smarter and more moral than the rest of us, who are we not to believe them?
DOCTOR TO YOSSARIAN [paraphrasing]: What if everybody believed that?
YOSSARIAN: Then I’d be crazy to believe anything different, wouldn’t I?
The authors almost immediately lost me with the phrase:
“..even the experts were shocked.”
They are evidently hanging with the wrong crowd as I heard such events being predicted many, many years ago.
No “expert” who matters was shocked by it, since they were either among the minority who were sounding the alarm ahead of time, or the majority who understood perfectly and who were working to help inflate the bubble and obscure the robbery.
As for the idiots who truly didn’t understand, did they have an epiphany in 2008 and move to determined opposition? No – they remain confused to this day. That’s why they’re irrelevant and worthless, and indeed objectively on the side of the criminals.
Picking up on the quoted reference to the Japanese tsunami, there are plenty of warnings, literally written in stone hundred or more years ago and dotted around the coast line of Japan,as to the dangers of tsunamis.
http://www.heraldtribune.com/article/20110421/WIRE/110429909/2055/NEWS?Title=Ancestral-markers-warned-Japanese-of-tsunamis
Now how does that effect the prdictability equation ?
The more and the clearer the warnings, the more defiant the belief that nothing bad will happen. ha ha ha.
This is the third conclusion that will be arrived at when the authors expand their study from roulette to real world events.
Something that stands firmly in the ground, sturdy and visible to everyone at all times to see in the location to which it refers ain’t so crude.
It is elegant; and a testament to the crudeness of our communication -available to small academic minorities calling themselves scientists for secrecy and fraud.
I don’t know what relevance this type of study has to anything except playing lotteries. My guess is none. For those seeking a lottery strategy, here is the best one: use a random number generator to pick one number every week. Check your ticket against the winning score. Go on with your life. Chances are overwhelming you will never win, but at least you won’t miss the investment.
The lottery analysis is based on the stationary random process and independent trials assumptions. If the frequency of occurance is also sloped downward, apparent peridocity appears in the autocorrelation function.
The major accidents cited represent examples of tightly coupled events within a non-stationary random process, whose probablities are zero but not predictable.
The effect on public opinion may be similar, but the processes are not.
I do believe this has both policy and personal implications. I see it every day in my job (I’m a physician).
People have a low probability event in their life and then they over react to this.
For instance, yesterday a family came to see me because they were worried their 15 year old son would have a heart attack. the reason? because a friend of a friend had a child with a heart attack. They have seen me several times for this, and thus finally yesterday I capitulated and did an EKG and cardiac enzymes. I refuse to allow an echocardiogram. A complete waste of money for this family.
====
To apply this study and it’s Japanese reactor example to my life: it would be illogical for me as a Minnesotan to oppose a nuclear reactor in my state solely based on the Japanese example. the reason: an earthquake and tsunami is impossible near me. this is not to say that I cannot oppose nuclear power, but only to say that I need be cautious about applying the Japanese situation to my state.
(on the flip side, though, I would say the Japanese and the Gulf of Mexico examples do show me that big business and govt cannot be trusted to do the right thing, and thus I need to be wary of them).
======
the pitfall of this study would be to use this data and apply it to our recent financial meltdown and to conclude, like our financial elite, that hoocoodanode and it was simply another 100 sigma event that could not possibly have been averted… and likewise no regulation is needed because it’s so unlikely to ever happen again.
of course this is the problem with all studies. Learning how and when to apply a study. I see intelligent people misapply studies all the time, even here sometimes.
Big typo in second paragraph!!!!
The probabilities are not zero but also not predictable.
One in a million frequently represents a guestimate which could be one in a trillion, one in a godzillian, but it is still non zero
The tsunami and the earthquake were, to all intents and purposes, a single event. Undersea earthquakes are usually or always accompanied by tsunamis.
The nuclear disaster was a very possible result of the earthquake / tsunami. It was contingent on the location of the nuclear plant and the sturdiness of the design. There were already questions about the design of the plant, so the disaster was not at all surprising, though not predictable either.
The article seems completely irrelevant to Fukushima. Gambling events are systematically randomized, and reality is not.
The article seems completely irrelevant to Fukushima. Gambling events are systematically randomized, and reality is not.
Perhaps people misunderstand the point of the article?
The issue is not about random vs nonrandom. The article is demonstrating PERCEPTION of probability, and not true probability.
The articles uses data from an event we KNOW is rare and random (about 1 in 8,000,000) to show that people’s PERCEPTION of the odds change based on past history when in fact they should not. One must control for many factors in order to prove that the people’s perception is changing, and also that it is not reasonable for their perception to change.
Regardless of what happens in the past, the future probability of winning the cited lottery is 1 in 8,000,000. But the article shows that this is not the subject cohorts’ calculations or behavior pattern (although I actually have issues with this data based on the confidence intervals… but we’ll go with the study here).
it is therefore important to know this fact when determining what we should do about other non-random rare events. in other words: if our perceptions change with regard to random rare events, it is logical (but not proven) to conclude that we likely have changed perceptions to nonrandom rare events as well.
Fukushima is/was a rare event. The fact that it is not random is immaterial. Our response to this rare event is possibly (if the study is to be believed) impacted by the change in perception elucidated in that study.
this does not mean that we should not act. only that we should understand that the rare event is, indeed, still rare. we are no more likely to have a Fukushima next year than we were to have one last year. Only our PERCEPTION of the odds of the event have changed.
but let me repeat so that nobody can misinterpret my words later: this does NOT mean that we should avoid action on GoM and Fukishima and the Financial Crisis.
===
lastly, it does work both ways. it is not only that subjects over-estimate the odds of certain things, they also underestimate.
Thus, one could easily argue that we as a society UNDERESTIMATED the odds of Fukishima/GoM/Great Recession, because we had a long string of days without a crisis. This string of “no problem” led us to improperly underestimate the odds of future problems and therefore we allowed our regulation/intervention/supervision to wane over time.
now we have had an event, and we have changed our perceptions of these events again. Interestingly, it does NOT mean that we all will overestimate the odds.
some people will over estimate, and some will UNDERESTIMATE again!!!!
the logic would go like this “well, now that we’ve had a Great Recession the big banks have learned their lesson and they won’t lever up again! thus, we’re less likely to have another 100 sigma event! we got that out of the way! whew!”
sorry for long rambling.
I think Fukushima, Macondo, Katrina and New Orleans levees, the 2007-9 financial crisis, and the recent tornado outbreaks outline the importance of regulation and engineering for three different types of systems:
1. Frequent, but local randomly located impacts;
2. Infrequent, but widespread impact; and
3. Man-made interconnected systems with a propensity for progressive collapse.
The recent tornado outbreak is an event that happens several times a year, so having tornados is normal and frequent. This one happened to be a bit worse than usual, but in the end only small areas were directly impacted. Warnings systems and hardened shelters keep loss of life to a relatively low amount while non-hardened property gets heavily damaged where a tornado touches down.
On the other hand, a Fukushima earthquake and tsunami combination is very infrequent, but actually inevitable so it is improbable that it happens at that moment but there is a very low probability that it would NOT occur over a period of several hundred years. As an engineer, it is inconceivable to me that the Japanese did not connect the dots of large earthquake, tsunami, and diesel generators at low elevation along a coast for a critical structure. If you are designing for an earthquake, then you have to design for the whle shebang since the big earthquakes in Japan occur along offshore normal faults in their subduction zone and therefore cause tsunamis. This is completely unlike California, where the big earthquakes occur on-land along transform faults that do not cause tsunamis. Therefore, tsunamis and earthquakes in California are really independent events which can be handled within their own little probability worlds.
I put the diesel generators at Fukushima (the failure of which is really the cause of the nuclear meltdown) in the same category as Macondo, New Orleans, and the 2007-9 financial crisis. In this case the failure is due to to probability of a confluence of human hubris, corruption, and stupidity with “random” negative triggering events. The human elements are essentially pre-positioning poorly designed, unstable systems prone to progressive collapse once failure is initiated and that only await a trigger to go off, somewhat like the design of a bomb.
The impacts of “improbable” events can be mitigated through the design of redundant, robust systems that account for major failure modes. However, as the author points out, people tend to discount the importance of this over time so we get actions like the repeal of Glass-Steagal since it was clearly not needed anymore because there hadn’t been a financial crisis for 60 years.
The article says: “Nuclear catastrophe, financial crisis and the like are things that even experts struggle to predict.” It’s difficult to predict the timing of these events, but not their eventual likelihood. Right now I predict another nuclear catastrophe and another financial crisis; anyone want to take the under?
Also the article posits that people are less likely to pick numbers from the previous lotto draw, yet relates the anecdote that a surprisingly large number of people pick ALL the numbers from the previous draw. This contradiction begs for explanation, does it not?
Goes back to the old rule: any discussion of statistics is in all probability inaccurate.
Wow, that conclusion has nothing to do with the study. It clearly sounds like someone wanted a (pseudo)scientific excuse to avoid regulating nuclear and financial matters, and dreamed up a lottery study to fit the part.
Earthquakes and financial crises are not uncommon events. The Earth will continue to quake, and if there’s a nuclear reactor on top of it, it generally won’t be a good thing. Financial crises occur because people in power decide to create the conditions for them, generally to their own benefit. These are not random events.
I think the conclusion was given as an example of the difficulty of inferring a general truth from more narrow ones, thus showing that even the authors do not escape the fallacies they are studying. A better conclusion would be that inference is hard, but a better understanding of statistical processes will help one with it. Thus, everyone should spend more time honing their reasoning skills if they want to make their life better. Etc., etc.
Any article about Lotto that does not provide pick numbers is worthless.
Just like CNBC.
Priceless dude.
@pebird
Read the article again, in one sense it is about gambling on or trying to predict random events. What you should be taking from it, as far as the lottery is concerned, is that there is no such thing as “pick numbers”. The result cannot be predicted. Therefore you may as well do your own set of random numbers or the same numbers each week. It makes no difference to your chance of winning.
Dear Fiendes;
Despite all the discussion about probability and statistics I see the point as being:”Perception tends to drive decisionmaking.” Being that the denizins of this and associated blogs have a high tolerance level for “conspiracy theorys,” the issues relevant to the theorys of Chomsky et. al. come into play. If a clever player grasps the implications of the Lotto study, he, she, it, or they would apply the lessons to “real life” situations. The recent calls for Austerity Spending Policy come to mind. To try to put a little perspective on it all, consider the following: A man staggers into a hospital with a bullet in his back. “They’re out to get me!” he croaks. The admitting interne is now faced with a dilemna. Send the man to the Knife and Gun Club meeting, or lock him up in the Secure E R as an obvious Paranoiac?
Oh well, the Trusty is telling me my time is up. See ya.
“Non-important” events are also hard to predict.
There’s one thing that intrigues me about Probabilities and Lotteries and I wonder if anybody has the answer. See, if we throw a coin a number of times, the probabilities of getting an equal number of draws for each side increases as the number of throws get bigger. (Ex. with 50 throws we may get 29 to 21 but with 1000 throws we may get 490 to 510, i.e. much closer to 50/50.) So things work out as if there was a memory somewhere taking notes and making sure a more of less precise result is attained if we make a big enough number of tries. My question arises in the sense that this could open the door for the manipulation of a Lottery, any lottery, even those where you see a number of numbered balls inside a cristal sphere and where there’s no human intervention whatsoever. How? Simply: you make the thing work many, many times, between public draws and you take your own notes. There you may notice that, for ex. the number 7, 34, 40, have been absent for many draws, which mean the chance of having them during the next draws is much bigger. But nobody but you knows that–the machine doesn’t discriminate between public and private draws, does it?. So, you haven’t even touched the balls, but you have cheated, you have manipulated results, you have made even the sharpest mathematician playing the odds get off the track–that if you can get your hands on the machine between public draws.
Sorry, Felix… Your results reveal:
1) The machine is failing to show the numbers 7, 34, and 40. This means these numbers will not show up, in future. If you have run the machine a few thousand times, then this is likely—but not proved.
OR
2) The machine is working properly, and you are seeing a short-term sequence. The probability of the numbers appearing is still the same as any other numbers appearing.
“(Ex. with 50 throws we may get 29 to 21 but with 1000 throws we may get 490 to 510, i.e. much closer to 50/50.) So things work out as if there was a memory somewhere taking notes and making sure a more of less precise result is attained if we make a big enough number of tries.”
felix,
Your assumption about the presence of a “memory” effect is wrong. There is a noise level associated with a given sample size; thus, for 50 throws, if you get 29 heads, you’d associate the extra 4 heads with the inherent noise in the system. Mathematically one can show that noise scales as the square root of the sample size. Thus, as the sample size increases, the relative ratio of the noise decreases, and you get closer and closer to the theoretical prediction of 50/50.
“this study shows that laypeople tend to draw strong conclusions based on few observations, and that biases are common and systematic when predicting improbable events.”
WOW… human nature exists! Really, somebody got paid for this “insight”?
For meaningful analysis Dan Ariely handles this territory much more scientifically with his books ‘Predictably Irrational’ and ‘The Upside of Irrationality’… and without the giveaway political commentary.
People typically operate on a fairly basic set of heuristics. This is not news. Of the varying definitions, I’ll use this one: “A rule of thumb, simplification, or educated guess that reduces or limits the search for solutions in domains that are difficult and poorly understood. Unlike algorithms, heuristics do not guarantee optimal, or even feasible, solutions and are often used with no theoretical guarantee.”
Here is a blatant propaganda bit:
“In a more general perspective, such biases may induce public opinion and the media to call for dramatic swings in policy in response to highly improbable events. Politicians are then under pressure to yield to popular demands for drastic regulation.”
The most obvious spin here is the use of the phrase “drastic regulation”. As far as I have observed the public is concerned about personal and public safety (not necessarily more regulations as it’s often that the existing regulations are not being enforced) and it’s the politician’s rhetoric and their spin-meisters who prattle and battle on the over-regulate vs under-regulate terminology axis.
The concern over managing public opinion reminds me of the book I am finally reading now, “Propaganda”, the classic by the master himself, Edward Bernays. The conclusion above is clearly poltiics masquerading as science, OR
in very simple words, I view the author’s conclusion as specious bullshit. And on that subject I recommend “On Bullshit” by Harry Frankfurt.
One last comment… as to the unexpected and unpredicted weather and disasters…. People who have some knowledge of history and geology know that “shit happens” all through time, often in bursts/clusters, mostly unpredictable and generally with terrible consequences for human populations. Without this sort of educational context it is easy to let emotions and apocophilia run wild. People have always struggled to find meaning in natural (or unnatural) disasters… and there have always been the hucksters and manipulators that prey on people’s fears at such a time to great profit. Literal “disaster capitalism” in many variations has been been practiced through the ages. Sometimes better policies result, but it seems that profiteering often leads the way.
Rumors of impressive technological advancement of the human race have been greatly exaggerated. If anything, the nuclear disaster at Fukushima demonstrates that nature will easily destroy everything that we build.
Until we learn to live in nature, rather than futilely trying to master her, we will continue to experience embarrassments such as Fukushima. Living in nature will obviously necessitate a radical reorientation of our economic system from its current obsession with growth, to a focus on sustainable development. Naturally, this will demand a complete eradication of this rapacious American-style form of capitalism. Anything short of that is likely to bring about our own extinction.
Psychoanalystus
Hows that VA gig doing ya, you seem sober / somber, in a non alcoholic way.
Skippy…Ditto your thoughts.
“…even the experts were shocked.” Which experts were those?
Any engineer would say, as many did, the probability of such a disaster is unity. It is “guaranteed” to happen, we just do not know when.
Part of engineering is risk assessment, though engineers refer to it as “reliability”, “mean time to failure”, “mean time between failures”, and such like. Basically, ANYthing will fail. The tricky parts are : 1) How long is this likely to do its job properly, and 2) What happens when this fails? Engineering consists of correcting problems before they occur.
The designs of most everything in the world are determined by penny-pinchers, not by engineers. At Three Mile Island, however, due to poor control board design and a failure to indicate the valve position properly, the operators did not know the valve was open. [http://www.nucleartourist.com/events/tmi.htm]
As I recall from the time, there was a light to indicate the valve was all the way open, but not a light to indicate the valve was all the way closed. In the TMI situation, both lights would have been off, indicating a fault condition.
Apparently, some suit somewhere, believing (Open=NOT Closed), decided two lights would be too expensive. Real valves have positions between all-open and all-closed: There is a continuum between open and closed, like a door; not on/off, like an electric switch.
This same non-intelligence is why the Fukushima diesel generators were exposed to flooding. As John W. Campbell pointed out, in an editorial in Analog Magazine, lack of forethought is nothing new. (His editorial discussed the 1965 East Coast power failure. One episode was diesel generators flooding out, because someone thought the flood-prevention pumps did not need to be on the generator. Ahem! Fukushima was built years later.)
As long as incompetent people make engineering decisions, there will be preventable problems!
This article makes no sense:
I’m amused to see probability assessment of a random event being used as justification to avoid reacting to failures when a chain of non-random events occur.
The ‘probability space’ of Fukushima is most certainly not ‘will a tsunami happen today?’ It’s something far more complicated and full of joint probabilities. To wit: should we build a power plant? If we do, how far from the shore? What backup generator? What material do we pick? What disaster recovery training do we provide?
The ‘probability space’ of financial regulation is even more full of joint probabilities. Each alteration of a regulation causes the actors in the market to behave differently. It is no natural phenomena or accidental phenomena that the market collapse happened–it can be directly traced to a series of human events predicated on their causes.
Lottery has such little to do with regulation that this argument is really nonsensical.
This is the perfect example of the Ludic Fallacy, as mentioned in Taleb’s “The Black Swan”.
The probabilities of the Lotto are known with great precision. No matter what happens with any draw, no new information is given about those probabilities. If there are 4 twenty-twos in a row, that gives zero new information about the next twenty-two.
Not only that, but the exact payout structure of the bet is also known: 99.9999999% of 100.000% loss of initial bet, infinitesimal chance of winning the full pot, some chance of a split pot in case of win).
With a nuclear power plant built on the coast on a faultline, the probability of a negative event is not known. It can only be modelled by engineers. When a negative event occurs, it then reveals that the probability distribution that enabled the go-ahead decision to build the plant was incorrect. SO unlike the gaming example quoted in this article THE OCCURRING OF THIS EVENT HAS CHANGED OUR KNOWLEDGE OF THE UNDERLYING PROBABILITY DISTRIBUTION. For example the previous model was based on the assumption that all the risk was in the reactor core and thus it was built in multiple layers. Noone considered the risk of the spent-fuel pool which was assumed would hold only a few rods at a time and only for a short time. Fuku reactor #4’s problems are from the spent fuel pool which is packed with nuclear fuel.
Likewise, the “payout” from a negative event is not known but can be unlimited.
Sorry, I didn’t say that the fact that a few numbers do not appear during a given number of draws means that they are ready to pop up in the next occasion. All what that means is that the probability that they will appear in the next draw, or during the next few draws, is better than that of those numbers that did appear often during the “test run”. (if you want to play the odds you’ll have to risk some of your money, anyway, and get some help computer–wise)Now, I went to my native country for some time and I took all the results of soccer games in the National League during the last four or five years–as they are available because of the National Soccer Lottery–and then I noticed that Locals tend to win 40% of the times, Visitors tend to win 20% and the remaining 40% is made of ties, no matter if I took one, two or four years into account. That was scary, the statistics were very precise in that regard. I’m not a mathematician but I guess a good one may get some good results playing either one or other kind of Lottery, with the apropriate software at hand–and if he’s willing to put his money were his… his numbers are, so to speak.
Now, to be clear, I’m aware that this can’t possible work in real life–otherwise every mathematical or computer in this world would be a billionaire and everywhere programs would be sold and bought To WIN THE LOTTERY. I have actually seen TV commercials to that effect but the fact that no one big Lottery winner has ever claimed to have used one of these programs, or simple probabilities, to win is enough proof that the noise Master refers to is big enough to throw off the best calculations you can make.